Trees Tidbit (10/25/2001)
Prepared by:
Joseph Malkevitch
Mathematics and Computing Department
York College (CUNY)
Jamaica, NY 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
A tree is a graph which is connected and has no circuits. That is, it is a diagram consisting of dots and lines which is in one piece and for which it is not possible to start at one of the dots (a vertex) and return to that dot using distinct lines (edges).
A typical example of a tree is shown below:
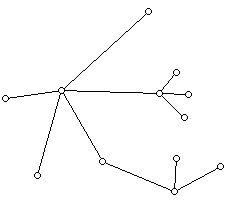
This tree has 12 vertices and 11 edges.
Here are some interesting facts about trees, that can be proved relatively easily.
1. There is a unique path between every pair of vertices in a tree.
2. Every tree has at least 2 vertices of valence 1. (The valence of a vertex is the number of edges that meet at that vertex.)
3. The number of vertices of a tree is one more than the number of its edges.
This result can be expressed in the form: V = E + 1, and can be thought of as a special case of Euler's polyhedral formula, V + F - E = 2 (Vertices + Faces - Edges =2) for a connected plane graph. A plane graph is one which can be drawn in the plane so that edges meet only at vertices. Trees are examples of plane graphs, and for any tree, F = 1.
4. If any edge of a tree is removed the graph is disconnected.
One can also assign weight to the edges of a tree to get a weighted tree.

Trees prove applicable in a tremendous variety of applied situations.
One of the nicest applications involves find a minimum cost spanning tree in a complete graph. A spanning tree for a graph G is a subgraph of the graph G which includes all the vertices. A minimum cost spanning tree can either be found by the algorithms of Joseph Kruskal or Prim. Kruskal's algorithm works by addition edges to a tree in order of smallest cost, so that a cycle never forms and all the vertices become included.
An example of a situation where one needs to find a minimum cost spanning tree is where one wishes to synthesize some kind of network at the cheapest cost, and where two locations do not have to be directly connected but can be reached from other locations by "relay" (i.e. going via other locations.)
Trees have a wide range of applications in computer science, where they play an essential role in the area of data structures. Tables, or matrices, when used as a data structure, often have many cells which are not used. Trees, though it may be harder to program algorithms associated with them, often are much more efficient. Among the kinds of trees that are interest computer scientists are binary trees (every vertex other than a leaf, a 1-valent vertex) has two descendants.
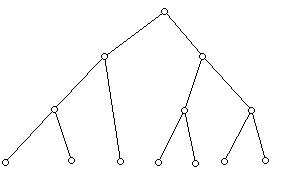
Trees have recently been used to construct phylogenies of species, genes, manuscripts, and languages. The idea is given two present day objects, say two genes, to find relate the two by some most recent common ancestor in a tree. The present day objects are thought of as the leaves of a tree, and then the internal notes of the tree are thought of as ancestors of the present day genes. Problems in molecular genetics have created a flood of interesting work on problems involving the distance between trees, finding a tree "closest" to a given set of trees, and a host of related problems.
Reference:
Bandelt, H., and A. Dress, Reconstructing the shape of a tree from observed dissimilarity data, Adv. Applied Math., 7 (1986) 309-343.
Bandelt, H., and A. Dress, Split decomposition: a new and useful approach to phylogenetic analysis of distance data,, Molecular Phylogenetics and Evolution 1 (1992) 242-252.
Buneman, P., A note on metric properties of trees, J. Combinatorial Theory (B), 17 (1974) 48-50.
Dress, A., Trees, tight extensions of metric spaces and the cohomological dimension of certain groups-a note on the combinatorial properties of metric spaces, Advances in Math., 53 (1984) 321-402.
Edelberg, M., and M. Garey, R. Graham, On the distance matrix of a tree, Discrete Math., 14 (1976) 23-29.
Felenstein, J., The number of evolutionary trees, Systematic Zoology, 27 (1978) 27-33.
Gusfield, D., Algorithms on Strings, Trees, and Sequences, Cambridge U. Press, New York, 1997.
Hakimi, S. and S. Yau, Distance matrix of a graph and its realizability, Quarterly of Applied Math., 22 (1964) 305-317.
Malkevitch, J. et al., For All Practical Purposes, (5th or earlier edition), W. H. Freeman, New York, 1999.
Warnow, T., Some combinatorial optimization problems in phylogenetics, in Graph Theory and Combinatorial Biology, L. Lovasz et al. (eds.), Bolyai Society Mathematical Studies, Volume 7, Budapest, 1999, 363-413.
Waterman, M., Introduction to Computational Biology, Chapman and Hall, New York, 1995.
Back to list of tidbits


