Four-Color Theorem Tidbit (09/13/2003)
Prepared by:
Joseph Malkevitch
Mathematics and Computing Department
York College (CUNY)
Jamaica, NY 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
A common way to assist people get a feel for world geography is to display the various countries on a (spherical) globe. To help with understanding which countries share a border it is useful to have countries on the globe which share a common boundary (an edge, in graph theory terminology) have different colors. What is the minimum number of colors necessary to color the countries on a sphere so that countries that meet along an edge get different colors? To answer this mathematical question for spheres is a bit of a nuisance because as one looks at a globe one can only see the countries on one hemisphere, because the other countries are hidden from view. Is there some way of displaying the information on a sphere in a more convenient way? In fact there is! The problem of coloring maps on a sphere can be reduced to the problem of coloring maps in the plane by a simple geometrical transformation.
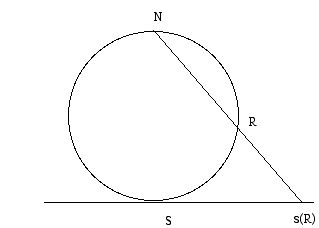
This approach to problem solving is typical of the way that mathematicians work. Taking a problem in one setting and trying to recast into an easier related setting. The transformation this time is know as stereographic projection. Take a sphere and let N represent its North pole and S represent its South pole. Now let P be a plane tangent (i.e. touching at exactly one point) to the sphere at S. If R is any point of the sphere except N, the image of R in P, which will be denoted s(R) will be the point where the line NR meets the plane P. The two dimensional analog of stereographic projection, which should make clear what happens in 3-dimensions, is illustrated in the diagram below:. Notice that points which are close to the North pole are transformed to points which are very far away from the South pole.

Although stereographic projection has a lot of fascinating properties, that make it a valuable transformation in analysis and topology, I will not explore these aspects of the transformation here. Suffice it so say, that if one has a drawing on the sphere which consists of dots and lines (a graph) which represents the outlines of countries then as long as one chooses the North pole N not to lie at a vertex or along an edge, then one gets a new graph drawn in the plane which will have the same properties for the purposes of coloring as did the original graph on the sphere.
Geometrical maps can have the complication, that the same country may consist of separate regions, as was the case with Pakistan when it was first created. For simplicity, we will only consider maps drawn in the plane so that each country consists of one connected region. A typical map of this kind is illustrated in the diagram below:
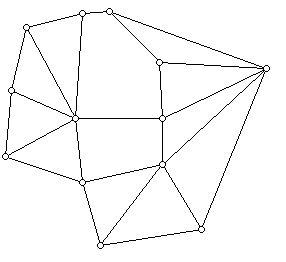
In abstract terms, we are given a connected plane graph whose regions (also called faces of the plane graph) we wish to color such that regions which share an edge must get different colors. If you want you can think of the region which surrounds all the other faces (usually called the unbounded or infinite face) as the ocean and require that this region be colored blue. By 1852 the following conjecture had already been made: All plane connected maps can be colored with four or fewer colors. This conjecture, posed by Francis Gutherie in 1852, came to be known as the four-color problem. It would elude solution until 1976, when Wolfgang Haken and Kenneth Appel solved the problem with the assistance of a computer. Although a newer and simpler proof has now been produced, by Neal Robertson, Daniel Sanders, Paul Seymour, and Robin Thomas, the use of a computer is still a required part of the proof.
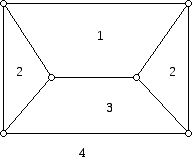
The graph below can be face colored with two colors using the two colors 1 and 2:
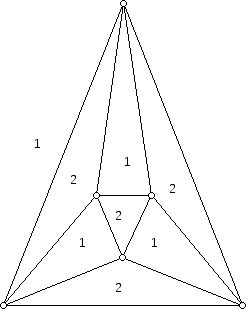
By contrast, the graph below can not be colored with two or three colors, but actually requires four colors, here, the numbers 1, 2, 3, and 4:
In order to make progress on the four-color problem some "simplifications" were made in the question being addressed. An example of such a simplification is working with plane maps with nice properties rather than "any old" plane map. For example, it is not difficult to "reduce" the general question of coloring the faces of plane maps with four or fewer colors to the problem of coloring the faces of a 3-valent plane map with four or fewer colors. (A 3-valent graph is one for which every vertex has valence 3, that is, there are 3 edges at every vertex.) Suppose G is a graph drawn in the plane for which every vertex has valence at least 3. An example of such a graph is shown in the diagram below:
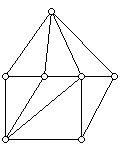
The graph above has three 4-valent vertices and one 5-valent vertex. We can now replace a vertex of valence i in this diagram with a face with i sides, bounded by 3-valent vertices as shown in the diagram below:
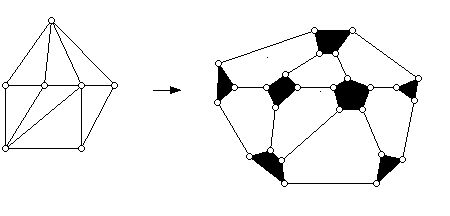
This construction results in a new plane graph all, of whose vertices are 3-valent. Note that we did not have to perform the "truncation" operation on the 3-valent vertices above, however, for purposes of illustrating the process this was done. If one can four color the faces of this graph, then one can four color the faces of the original graph by shrinking down to a single vertex the faces that are shown in black on the right above. Remember that faces that touch at a vertex, after the shrinking process, but do not share an edge can be colored the same color. Some plane graphs have vertices of valence 1 or valence 2. One can also transform such graphs to new ones where the vertices of valence 1 and 2 are eliminated (this is done by creating faces with 1 side or 2 sides), and where the new "graph" (strictly speaking a multigraph, since there may be more than one edge joining the same pair of vertices) is plane and only has 3-valent vertices. Again, the original graph can be colored with four or fewer colors when the new one can. Thus, we can reduce the problem of coloring plane graphs with four or fewer colors to the problem of coloring plane 3-valent graphs with four or fewer colors.
Over a period of time, it was shown that if one could solve the 4-color problem for the plane graphs which arise as the edge-vertex graphs of 3-valent 3-dimensional convex polyhedra, then one could solve the problem for all plane graphs.
The methods used to solve the four-color problem are rather complex in detail, but it is possible to say something about the ideas involved.
First, instead of showing that the faces of every plane graph could be colored with four or fewer colors, the "dual problem" of coloring the vertices of a plane graph with four or fewer colors was studied. For a vertex coloring of a graph (one can color the vertices of any graph while it is meaningful to discuss face coloring problems only for plane graphs) one assigns a label to each vertex so that vertices joined by an edge get different labels.
Second, one makes use of Euler's formula. This result says that if one has a plane graph which is connected (i.e. consists of one piece) then V + F - E = 2 where V denotes the number of vertices of the plane graph, F denotes the number of its faces, and E denotes the number of its edges. This remarkable formula, which might have been known to ancient geometers, seems to have eluded all researchers until Euler noted the relationship in 1752 (in the context of 3-dimensional polyhedra).
Third, an attempt was made to understand the properties of what the smallest plane map which failed to be colorable with four colors would be. This approach yielded a series of results saying that the smallest map which could fail to be colored with four colors would have to have an increasingly large number of regions.
Forth, using an approach suggested by the German mathematician Heinrich Heesch, the concepts of "discharging" and "unavoidable" collection of configurations were pursed. Informally, the concept of an unavoidable set of configurations is that any 3-valent plane graph which is 3-connected (hence there is some 3-dimensional convex polyhedron which realizes the graph) must contain a configuration in the unavoidable set. The concept of discharging is a way of showing that any minimal counterexample to the four color conjecture must have an element in a specified unavoidable configuration. The need for a computer in the two proofs that have been found for the four-color problem is a result of the vast number of cases that must be considered in the interplay between discharging and the theory of unavoidable sets.
It is widely believed there will be no "short" proof (i.e. computer free) of the four-color conjecture.
References:
Appel, K. and W. Haken, Every Planar Map is Four Colorable, American Mathematical Society, Providence, 1989.
Fritsch, R. and G. Fritsch, The Four-Color Theorem, Springer-Verlag, New York, 1998.
Grünbaum, B., Convex Polytopes, Wiley-Interscience, New York, 1967. (Second edition, 2003.)
Jensen, T. and B. Toft, Graph Coloring Problems, Wiley, New York, 1995.
May, K., The origin of the four-colour conjecture, Isis, 56 (1965) 346-348.
Mirzakhani, M., A small non-4-choosable planar graph, Bull. Inst. Combin. Appl., 17 (1996) 15-18.
Mohar, B. and C. Thomassen, Graphs on Surfaces, John Hopkins University Press, Baltimore, 2001.
Robertson, N., and D. Sanders, P. Seymour, R. Thomas, The four color theorem, J. Combinatorial Theory Ser. B. 70 (1997) 2-44.
West, D., Introduction to Graph Theory, Second Edition, Prentice-Hall, Upper Saddle River, 2001.
Wilson, R., Graphs Colourings and the Four-colour Theorem, Oxford, Oxford, 2002.
Wilson, R., Four Colors Suffice, Princeton U. Press, Princeton, 2002.