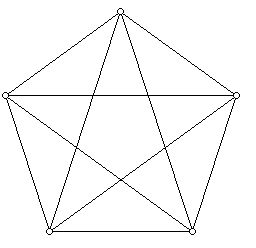
Figure 1 (A graph, consisting of dots joined by line segments.)
Tidbit 33: A Single Graph Can Have Inequivalent Embeddings in the Plane
Prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Mathematics is often concerned with when things that look different are really different or are in some natural sense the same. Though the fractions 3/6 and 1/2 look different, we can typically use 3/6 and 1/2 interchangeably.
A graph is a diagram consisting of dots and lines, such as that shown in Figure 1 below:

Often graphs can look quite different but have the same structure, that is, are isomorphic. Thus, for example, in Figure 2 below there are several representations of the 3-dimensional cube. In fact, all these drawings show isomorphic graphs. Though the graphs look a little different, they have the same "structure."
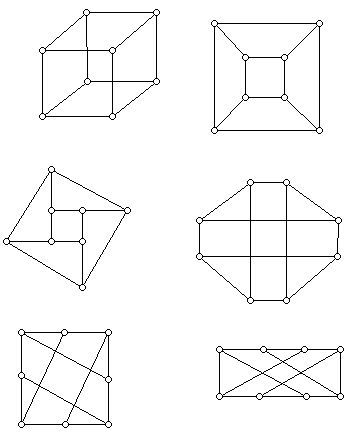
An interesting aspect of graphs is that sometimes they can be drawn in the plane so that edges meet only at vertices. No such drawing of the graph in Figure 1 exists but there are two such drawings in Figure 2, the diagram in the first row on the right and the one in the second row on the left. When a graph is drawn in the plane it is said to have been embedded in the plane or have a plane drawing. A planar graph G is one for which one can draw a graph isomorphic to G embedded in the plane. All the graphs in Figure 2 are planar but the graph in Figure 1 is not. A graph drawn in the plane so that edges only meet at vertices is often called a plane graph.
In addition to vertices and edges plane graphs cut up the plane into regions which are called the faces of the embedded graph. The "infinite region" that surrounds the graph is also a face, sometimes known as the infinite face or unbounded face. Each face has a certain number of edges in its boundary. The two plane drawings of the cube show 6 faces,
each of which has 4 sides.
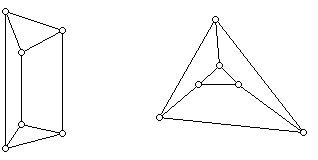
In Figure 3 there are two plane drawings of a graph which look rather different but are isomorphic as graphs. Furthermore, each of the graphs has two faces which have three sides and three faces which have four sides. The graph on the left has an infinite face with four sides, while the one on the right has an infinite face with three sides.
Are there graphs which can be drawn in the plane in such a way that one can get two (or more) drawings of the graphs which are isomorphic as graphs but which have different face structures? The perhaps surprising fact is that this can happen. A drawing of a graph with two different ways to embed it in the plane from the point of view of the structure of its faces is shown in Figure 4.

In Figure 4, the graph on the left has 4 faces, one 3-gon, two 5-gons, and a 7-gon. The graph on the right has one 4-gon, two 5-gons and one 6-gon. (An i-gon is a face with i sides.) Sometimes a plane graph together with the faces it creates as a consequence of the way that it is embedded is called a map. The example in Figure 4 shows that two plane graphs can be isomorphic but the maps that they create need not be isomorphic! This seems a surprising possibility until one gets used to it. The next natural question is to ask if, when a plane graph has certain properties, the map it creates when embedded in the plane be "unique." The two embeddings of the graph in Figure 3 look different; the maps they create are isomorphic, as maps.
It turns out this question was answered by the American mathematician Hassler Whitney. He showed that if a plane graph H has the property that for any two of its vertices p and q there are at least three paths from p to q whose only vertices in common are p and q (when this happens the graph is called 3-connected), then drawings of H may look different (as in Figure 3) but as maps they will be isomorphic.
Amazingly, it turns out that graphs which are planar and 3-connected
are the edge-vertex graphs of convex 3-dimensional polyhedra. This unexpected result of 20th century geometry was discovered by the great geometer Ernst Steinitz. However, it was Branko Grünbaum and Theodore Motzkin who reformulated what Steinitz did in the language of modern graph theory. The significance of Steinitz's Theorem is that for working on the combinatorial theory of 3-dimensional convex polyhedra one does not have to think about these objects in 3 dimensions, but it is sufficient to work with the family of planar graphs, which are 2-dimensional, the 3-connected plane graphs.
For 3-dimensional convex polyhedra the phenomenon we saw in Figure 4 can not occur. Graphs of such polyhedra, due to Whitney's work can in essence be embedded in the plane only in one way. The number of sides of the infinite face may vary, but any two drawings of such a graph in the plane will be isomorphic both as graphs and as maps. The proof of Steinitz's Theorem builds on the fundamental result about graph theory and polyhedra known as Euler's Polyhedral Formula.
Reference:
Grünbaum, B., Convex Polytopes, (Second Editon), Springer, New York, 2003.
Malkevitch, J., AMS Feature Column, Euler's Polyhedral Forumula, I
Malkevitch, J. AMS Feature Column, Euler's Polyhedral Formula, II.