Adventures in Geometry for Third Graders (2/20/2000)
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computing
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Dear Parents,
The "facts" of Mathematics, unlike those of science, do not have to be revised in
light of new empirical discoveries. Once mathematics is proven valid, it remains
so. This creates a problem for teachers of mathematics at all grade levels since
new mathematical ideas are being discovered all the time and never replace what has come before,
only augment it. This especially provides challenges for what new mathematics to
teach in the lower grades since youngsters, say in the third grade, do not have a
lot of prior mathematical knowledge at their disposal. Thus, it is especially nice when, from
time to time, it becomes possible to find use for skills traditionally taught in
the lower grades on a topic that is also at the frontiers of the kinds of problems
mathematicians think about. But what is it precisely that mathematicians do?
If you wanted to give a simple definition of what a mathematician does, to accompany
the simple definitions that define the work of a carpenter, pharmacist, or doctor,
what definition would you offer? Mathematicians are not experts at balancing check
books, nor are they better at arithmetic in general than most people. Mathematicians are
experts in the science of studying patterns. For example, they study patterns in
numbers, patterns in knots, patterns in data (statistics) and patterns in shapes
(geometry), to give but a small sample of what mathematicians study.
A good example of the way that mathematics helps with understanding general phenomena
by abstracting from more common ideas concerns the idea of "distance." We are accustomed
to thinking about the distance between two physical locations such as our home and where we work or where our child goes to school. In conjunction with distance we
use the terms near and far to convey the notation that some locations are close together
while others are not close together. Once having thought of the notation of "closeness," why limit it to physical locations? Can we make "sense" out of asking questions
such as "Is French closer to Italian than it is to Spanish?" Is Cousin Rachel a closer
relative than Cousin Jack? Is emerald green closer to mint green than sky blue is
to robin's egg blue?
What is there about physical locations that makes it possible to assign a distance
between them? Distances are positive numbers or zero, and when the distance between
two places is zero they are the same. Furthermore, the distance between A and B is
the same as the distance between B and A. The one property of distance that may not come
to mind immediately, but is an essential one, is illustrated by the diagram below,
the distance from A to B added to the distance from B to C is at least as large as
the distance from A to C. (Distance satisfies the "triangle inequality.")

However, adults are familiar with many subtleties of the distance notion. We know
that the distance in a car between two places, the "distance" walking between two
places, and the "distance" between two places as the crow flies are not the same!
This is true for cars because cars have to obey one-way street constraints. When walking between
two locations in the country one may be able to go as the crow flies, but in an urban
environment one must move along the streets, which are often laid out in a grid structure.
Mathematicians long ago realized that these subtleties mean that there is no single
way to find the distance between two locations. The usual distance is Euclidean distance
(based on the Pythagorean Theorem: in a right triangle: the square on the hypotenuse equals the sums of the squares on the other two sides of the triangle (the legs)).
However, in the picture below, suggesting the grid system of blocks typical of many
urban and suburban environments) the cost of a taxicab ride from A to C is not proportional to the crow flies distance (Euclidean distance) but to the so-called taxicab
distance, which involves moving along lines consistent with the grid system. Thus,
as the crow flies the distance from A to C is 5 (since the square root (32 + 42) = square root (9 + 16) = square root (25) = 5), while the taxicab distance from
A to C has length 7 since we must follow the grid system. Note that while there is
only one route that achieves the crow flies distance of 5, there are actually 35
different routes of taxicab distance 7 from A to C! (Check for yourself.)
(The "coordinates" in this diagram, i.e. the names given to the points, are all referred
to the origin (0, 0). The first number gives the number of steps from the origin
in the easterly direction; the second number gives the number of steps from the origin in the northerly direction.)
In fact, it turns out there are infinitely many different ways to define "distance"
between points in a plane that obey the abstract rules listed above that a "distance"
should obey.
Questions about the "taxicab" plane, geometry on a discrete grid of squares, enable
students in lower grades to see the interaction of new ideas and reinforce skills
that they are learning but often do not have that many contexts in which to see that
these skills are really of value. (The value of reading is apparent to students in lower
grades but in their own view how does knowing addition, subtraction, etc. facts really
make much difference?)
In addition to using reading skills to figure out what calculations should be done,
the project included here shows the value of having names for position locations
(coordinates), of addition and subtraction, of combinatorics (fancy counting). However,
there is a major application of mathematical analysis in the background. This is the
Traveling Salesman (Salesperson in these times) Problem (TSP). The TSP is the problem
of finding the minimum "distance"
(distance being defined in terms of time, weight, cost, or some other quantity of
interest) route which starts at a "home" location and visits each of a collection
of sites once and only once. In a child's world this might involve "efficient" routes
for delivering papers on a paper route or for trick-or-
treating. In a parent's world this might involve the best route for picking up kids,
taking them to a movie and bringing them back to one's home, or finding the fastest
way to visit the library, the supermarket, the flower store, the stationary store,
and return home. However, and most importantly, the TSP is involved in designing efficient
routes for picking up mail from letter boxes (by the US Postal Service), the efficient
retrieval of coins from pay phone booths by a phone company, the pickup of hardcopy ATM records from sites where ATM machines are located, or the design of school bus
and camp bus pickup routes. These problems have routing conspicuously placed in the
application environment. However, probably the most common situation that requires
the solution of the TSP seems to have little to do overtly with routing: the manufacture
of integrated circuits (chips)! Chip manufacture requires the connecting up of very
miniaturized components located at various places in a grid. A laser starts at "home," carries out a sequence of connections and
returns to "home" in the minimum amount of time. Not only is this a TSP but also the
distance involved that is to be minimized (thereby minimizing time) is taxicab distance!
Doing mathematics with your kids is great fun.
Enjoy!
Worksheets
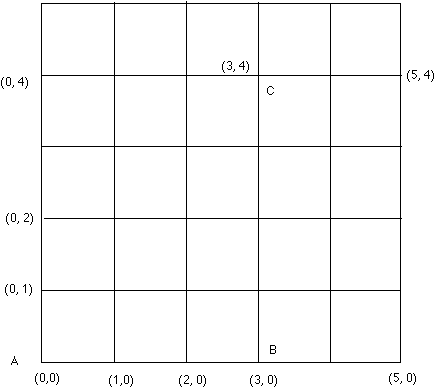
The map below shows the location of the houses of the friends Alan (A), Bob (B), Cathy
(C), David (D) and Ellen (E).

Part 1
1. If one walks a shortest route from C to A, how many blocks does one go?
2. If one walks a shortest route from C to B, how many blocks does one go?
3. If one walks a shortest route from C to D, how many blocks does one go?
4. If one walks a shortest route from C to E, how many blocks does one go?
The table below can be used to record the shortest distance in walking between the
houses of the friends:

Extra copy:
 Extra copy of the map:
Extra copy of the map:

Part 2
Next to the locations of the friends' homes are shown names for these locations which
help speed up finding the distance between the locations. Can you see how? Names
of this kind are known as co-ordinates for the points.
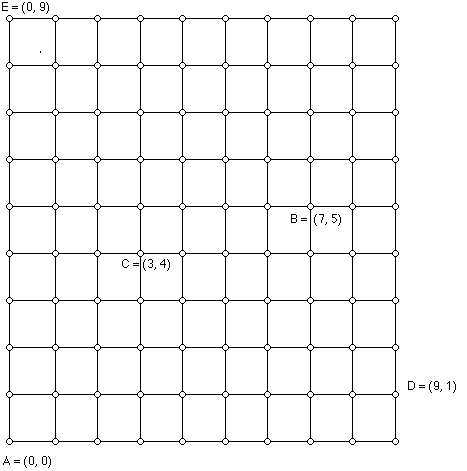
 Use the coordinates to find the distance from A = (0, 0) to F and G on the map below.
Use coordinates to find the distance from F to G, from G to D and from D to F.
Use the coordinates to find the distance from A = (0, 0) to F and G on the map below.
Use coordinates to find the distance from F to G, from G to D and from D to F.

Part 3
1. How many different shortest routes are there from A to E?
2. How many different shortest routes are there from E to C? Are you surprised?
3. How many different shortest routes are there from D to B? Are you surprised?
 Part 4
Part 4
1. Alan is planning to go trick or treating, starting at his house and to visit the
houses of four friends (B, C, D, and E), then returning home. What is the shortest
route he can follow for trick or treating?
2. Can Alan find the shortest route by first going to the house of the friend whose
home is closest to his, then going from there to the nearest by house, and so on,
until he returns home?
Part 5
The same ideas that come into play in trying to find short trick or treating routes
come into play in the work of businesses and governments.
Example 1:
Think of A as the location of the post office. Think of B, C, D, and E as the locations
of mail boxes where people have put letters they wish to mail. The post office worker
needs to find a short route for picking up the letters from the boxes and taking
them to the post office.
Example 2:
Think of A as the location of a school. Think of B, C, D, and E as locations where
school children wait for the school bus to take them to school. The school officials
must find a short route for picking up the kids and bringing them to school.
Example 3:
Think of A as the location of the phone company. Think of B, C, D, and E as the locations
of pay phone booths where people have deposited coins to make their phone calls.
The phone company needs to find a short route for picking up the coins from the phone booths and bringing them to the phone company office.
Example 5:
Think of A as the location of an oil company. Think of B, C, D, and E as locations
of homes where oil deliveries must be made. The oil company must find a short route
for its truck to use to deliver the oil before returning back to its home base A.
Challenge Problem:
Can you think of other examples of this kind where one wants to find a short route
to visit several locations and return back to the starting location using as short
a route as possible?
Return to Joseph Malkevitch's Home Page




 Extra copy of the map:
Extra copy of the map:
 Use the coordinates to find the distance from A = (0, 0) to F and G on the map below.
Use coordinates to find the distance from F to G, from G to D and from D to F.
Use the coordinates to find the distance from A = (0, 0) to F and G on the map below.
Use coordinates to find the distance from F to G, from G to D and from D to F.
 Part 4
Part 4