Review for Final Examination (Fall, 2008)
Mathematics 488 (Digital Codes)
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malice/
1. Find the value of the numbers below:
a. mod 6 b. mod 10 c. mod 4
i. 13
ii. -22
iii. 153
iv. 25
v. -37
2. Which of the pairs below are equivalent mod 8?
a. 5, 32
b. 49, -21
c. -23, -2
d. 23, -5
3. Using the zipcode dictionary from the digits 0 - 9, write down the bar representation (including guard bars and check digits) for:
a. 11432-0001
b. 11621-3279
4. Intellectual property is protected in American society in various ways. What kinds of property are protected by copyright, patent, and trade secrets? Give some examples of intellectual property that are protected by each of these forms of protection.
5. Determine the check digit (?) for the "fake" credit card numbers below:
a. 7789-1234-5678-215 (?)
b. 7789-4321-5178-915 (?)
6. Determine if the "fake" credit card number below is legal. If it is not what check digit should there be to make it legal.
a. 5234-1231-6587-3321
b. 7799-4323-5965-1112
(If the number is not correct, what digit has to be placed in the last position to make it correct?)
7. Compute the Hamming distance between the following strings of the same length:
a. 01100011 and 11101110
b. 11001111 and 11001101
c. ATGTTAG ATGTATG
d. TAGTAGTTT CATTTATGT
e. 21213366445565 21211223345575
f. ++++***++ ++****+++
g. 121110 212222
8. What is the decimal check digit associated with these (not all real) zipcodes:
a. 11451-0001
b. 11753-0321
c. 67544-1215
9. Design a Huffman code for items that must be coded and have the following frequencies:
a. 1, 3, 4, 5, 6, 11, 12, 30, 100
b. 1, 100, 7, 3, 14, 54
c. 1, 2, 4, 8, 16, 32, 64
d. 1, 1, 3, 3, 4, 5, 12, 56, 100
Note: For each of the above cases how many bits are required for a block code? How many bits are required when the Huffman code is used? How many bits are saved by using compression?
10. Compute the frequencies of the digits in the numbers below and then design a Huffman code to compress the information:
a. 1143325443244355552550505
b. 66607600067988899000000000660000000
11. Construct a Gray code for:
a. The permutations of the symbols 1, 2, a.
b. The binary sequences of length 3.
12. Draw the graph of a combinatorial:
a. 3-cube
b. 4-cube
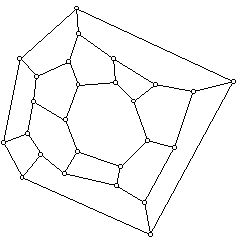
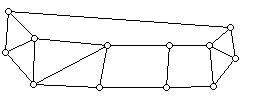
13. Find a hamiltonian circuit for the graphs below by wiggling the edges which make up such a circuit:
a.

b.
14. What would the check digit (?) be for these (non-real) Universal Product Codes:
a. 0 12345 67890 ?
b. 0 50743 21502 ?
c. 3 08694 23052 ?
Are these legal UPC numbers?
a. 4 21343 34219 8
b. 0 12344 56789 2
15. Determine if the following are "legal" ISBN numbers.
a. 1-55953-407-9
b. 0-13-309600-9
c. 0-13-100191-3
If any of the check digits above are not correct, determine what would be the correct digit for the prior numbers.
16. Which if any of the codes below are prefix free?
a. 0, 1, 11, 01, 10
b. 00, 10, 110110, 011, 0101
c. aab, aaab, bba, bbba
17. What are some new technologies that have been supported by error correction technology?
18. What are some new technologies that have been supported by data compression technology?
19. What are some of the purposes to which codes are put?
20 What are some government uses of codes?
21. What are some private corporation uses of codes?