History and Philosophy of Science
Review for Final Examination (Fall 2007)
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
1. Name some famous mathematicians who were also famous physicists.
Know the names of some famous Greek or "culturally Greek" mathematicians.
2. Can one define every term one uses in a mathematical system?
3. Find the value in decimal notation of the following numbers expressed in other bases or notations:
a. DCCLXXIV
b. MMDCXLVI
c. (110111)2 =
d. (1001)2
e. (1001)3
f. (132)4
g. (1202)3
h. g. (1202)4
4. Write the following fractions as Egyptian Fractions (use the Sylvester-Fibonacci method):
a. 3/14
b. 24/31
c. 11/19
5. Find, if any, the rational roots of:
a.

b.
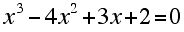
c. Apply Descartes Rule of signs (or its extension) to the above equations to try to determine how many:
i. Positive real roots the equation has.
ii. Negative real roots the equation has:
6. Use synthetic division to find the quotient and remainder when:
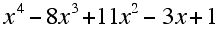
a. Is divided by x - 2
b. Is divided by x + 3.
4. Use synthetic division and "direct computation" to find the value of:
a. f(5)
b. f(-3)
c. f(3)
where:

7. Give a brief description of the role of the mathematical understanding of the parallelism concept in shaping the development of non-Euclidean geometry. Give a statement of the the modern version of Euclid's 5th Postulate.
8. Briefly discuss the difference between progress in science versus progress in mathematics. (You may wish to use such terms as inductive investigations, deductive investigations, experimentation, verifiability, a theory vs. a theorem, etc.)
9. Are there problems which are so hard that a computer can not solve them? Are there statements that can not be proven? (What is the difference between the issue of a statement being true or false versus whether or not it can be proven?)
10. What is the Cayley-Klein Model for the Bolyai-Lobachevsky plane?
11. Is 1/4 + 1/4 = 1/2 an Egyptian fraction decomposition of 1/2?
12. Compute the value of the following determinants:
a.
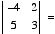
b.
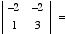
c. Use determinants to find the equation of the line through:
i. (2, 3) and (-3, 5)
ii. (-1, 0) and (2, 7)
13.

14. Compute the Euclidean, taxicab, and max distance between the following points:
a. (2, 2, 3) and (3,2, -1)
b. (3,9) and (2, -4)
c. (-1, 3) and (-7, -4)
d. (2, -4, 6) and (11, 4, -5)
15. Compute the Hamming distance between:
a. (111001110) and (111010111)
b. TTCGGCTAT and TTCCATTGT
d. attends and retains
16. Give a modern statement equivalent to the 5th postulate of Euclid.
17. Give an example of an infinite projective geometry.
18. Is the sphere with diametrically opposed points an example of a Euclidean, projective, or hyperbolic geometry?
19. Briefly describe the difference between geometry thought of as a branch of mathematics and geometry thought of as a branch of physics.
20. What topics did you enjoy in this course?
21. What topics were you disappointed because they were not treated?
22. What role do axioms play in a mathematical system?
23. What mathematicians were you hoping to learn more about but were not mentioned in the course?