Sheet Z (Mathematics 244-Geometric Structures)
(Taxicab Geometry)
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computing
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
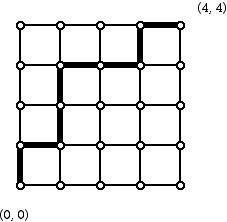
1. How many different paths that move along integer valued horizontal or vertical lines are there that move east or north that join (0, 0) to (4, 4)?

(A typical example of such a path is shown with thick segments above.)
2. a. Draw an equilateral triangle with side length 3 one of whose vertices is (0, 0)?
b. Draw an equilateral triangle with side length 3 one of whose vertices is (-1, 0)?
c. Draw an equilateral triangle with side length 3 two of whose vertices are (-1, 2) and (0, 0)?
3. Find (if they exist) the points where the circle of radius 2 center at (1, 0) intersects the circle of radius 2 centered at (1, 1)?
4. Find (if they exist) the points where the circle of radius 4 center at (0, 0) intersects the circle of radius 6 centered at (-1, 1)?
5. Given the points (0, 0) and (4, 4) what point(s) will form an equilateral triangle with these in the Euclidean plane? Given the points (0, 0) and (4, 4) what point(s) will form an equilateral triangle with these in the taxicab plane?
6. Is it possible to have three points A, B, and C which are simultaneously vertices of equilateral triangles in the Euclidean and taxicab planes?
7. Find those points in the taxicab plane the sum of whose distances from (-2, 0) and (2, 0) is 8. What would you call the analogous collection of points in the Euclidean plane?
8. Imagine that one has a set of points S that you can think of as the location of post offices. The Voronoi diagram for S shows those points that are closer to a particular post office than to another post office. The Voronoi diagram will depend on the distance function that one uses. For the Euclidean distance it can be seen that the Voronoi diagram consists of convex regions, some of which may be unbounded.
a. Draw the Euclidean Voronoi diagram for:
i. (0, 0) and (4, 2)
ii. (0, 0) (4, 2) and (-2, 6)
iii. (0, 0) and (6, 6)
iv. (0,0), (6, 6) and (-2, -4)
v. (0, 0), (6, 6) and (-2, -8)
b. Draw the taxicab distance Voronoi diagram for the same point sets as above.