Sheet C (Geometric Structures)

Polyominoes

prepared by:

Joseph Malkevitch
Department of Mathematics and Computing
York College (CUNY)
Jamaica, New York 11451


Email: malkevitch@york.cuny.edu

web page:
http://www.york.cuny.edu/~malk

Definition:

A polyomino is a plane geometric figure obtained by joining 1x1 squares edge to edge.

The diagram above shows a typical polyomino. Note that some polyominoes with enough square cells can have "holes."

Definition:

A polyomino with n-squares is known as an n-omino. Pentaminoes are polyominoes with 5 squares. The polyomino above is a 4-omino or tetramino.

1. Draw all the polyominoes with:

a. 1 square b. 2 squares, c. 3 squares d. 4 squares e. 5 squares.

2. What rectangles have dimensions with the potential that they can be decomposed into pieces which correspond to each of the pentominoes? (Put differently, what dimension rectangles can be "tiled" with a copy of each of the different pentominoes?)

3. Do all the different pentominoes have the same perimeter? If not, what different perimeters are possible?

4. Some hexaminoes can be folded on the edges that the squares meet at to form a cube. Do all of these hexaminoes have the same perimeter? If so, can you explain why?

5. If one cuts the top off of a square pyramid at the half-way mark down the segment joining the vertex of the pyramid and the center of the bottom square

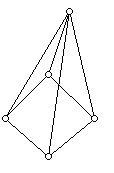
(Note a pair of edges appear to intersect, but, in fact, this is not a vertex of the graph involved.)

one obtains a solid with six faces which are 4-gons, and where every vertex has three line segments at it. Thus, the solid is a combinatorial cube. Draw several nets of the resulting solid.

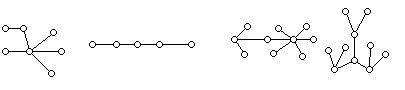
6. The diagram below shows four different tree graphs (e.g. connected, no circuits). Count the number of vertices and edges of the trees involved. Do you see a pattern?