
Geometric Structures (Math 244)
Review Examination II (Spring 2005)
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
joeyc@cunyvm.cuny.edu
web page:
http://www.york.cuny.edu/~malk
1. Give a precise statement of Desargues Theorem and draw a diagram which illustrates the theorem.
2. How many (internal) diagonals are needed to triangulate a simple n-sided polygon using the existing vertices of the polygon?
3. a. What is the interior angle of a regular 8-gon? b. How many internal diagonals are required to triangulate such a polygon?
4. Draw a non-convex plane simple 9 sided polygon?
5. Given the simple polygon below:
a. How many sides does this polygon have?
b. Triangulate the polygon using its existing vertices. How many triangles are created? How many diagonals are used.
c. Draw the visibility polygon from vertex o.
d. Draw the visibility polygon from vertex 3.
e. Using your triangulation from b., color the vertices of the triangulated polygon with 3 colors. What number of guards does this coloring lead to for guarding this polygon? Can you find fewer vertex guards than this number to guard this polygon?
f. Using guards who are not located at vertices, what is the fewest number of guards that you need to guard this polygon?

g. Are any of the vertices of the above polygon ears? (Recall the definition: x is an ear of a polygon if the line segment joining the two neighbors y and z of x in the polygon is an interior diagonal of the polygon.)
h. Can you draw a 8 sided polygon with exactly 2 ears? Can you find a family of polygons with n sides with exactly two ears?
6. a. For each graph below, determine if the graph is plane, planar, non-planar.
If the graph is planar but not plane, redraw it as an isomorphic plane graph.
b. How many vertices and edges does each graph have and what is the degree (valence) of each vertex of the graph.
c. Compute the values of vi (the number of vertices with degree i) and pi (the number of faces with i sides) for each graph.
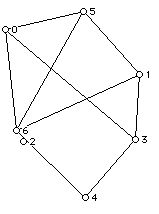


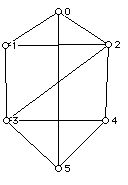
d. For each plane graph above how many sides does the infinite face have?
e. Which of the graph above are 3-connected?
7. a. Write down the multiplication and addition table for GF (5) = Z5.
Note: Below, all coefficients and numbers are in Z5.
b. Write down the points on the line x + y = 4 in the affine plane whose points are ordered pairs from Z5.
c. Write down a line parallel to the line above and goes through the point (1, 1).
d. What line corresponding to the line in b. which is in the projective plane with 31 points associated with the 25 point affine plane. (Hint: the points of this projective plane are ordered triples (x, y, z) taken from Z5.
e. What line passes through (1, 2, 1) and (2, 1, 2)?
f. At what point do the projective lines x + y + z = 0 and 2x + y + 3z = 0 meet?
g. List all the points on the line x + y + z = 0. (Hint: There are exactly 6 points, one with z = 0 and all the others with z = 1. Remember, for example that the point (2, 0, 3) is the same as the point (4, 0, 1).)
8. Find the roots if any, of the polynomial: x2 + x + 1 = 0. (Example: 2 is not a root because 2x2 + 2 + 1 is congruent to 2, not 0, modulo 5).
9. Since x2 + 4x + 1 = 0 has no root in GF (5), we can construct a finite arithmetic with 25 elements where the numbers have the form a + bΔ where Δ2 = -4Δ - 1 = 1Δ + 4. Remember that in GF (5) "-3" = "2" and "-2" = "3" and "-4" = "1."
In this field find:
a. The sum of 2 + 4Δ and 3 + 2Δ and the product of these two numbers. (Hint: Treat the terms like polynomials but use the fact that the coefficients are in GF (5) and also that Δ2 must be replaced by 1Δ + 4.)
b. Repeat for 1 + 4Δ and 4Δ.
10. Draw a simple polygon that requires exactly 3 vertex guards.
11. State Victor Klee's Conjecture (now the "art gallery theorem" about guarding n-sided polygons?
12. How many many vertex guards are required for a triangular art gallery with a single square pillar?