Guards
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
joeyc@cunyvm.cuny.edu
web page:
http://www.york.cuny.edu/~malk
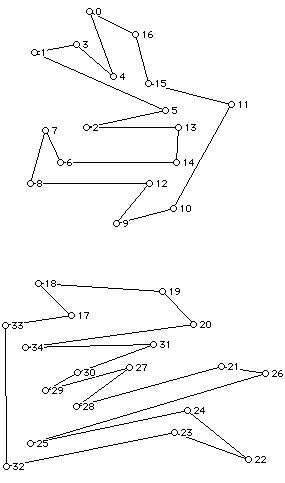
1. For each of the two plane simple polygons below:
a. Determine how many sides the polygon has?
b. Determine how many vertices the polygon has?
c. Draw the visibility polygon from the lowest numbered vertex of the polygon.
d. Triangulate the polygon using existing vertices in two different ways.
e. Use a 3-coloring of the vertices of the triangulated polygons to determine the number of vertex guards needed to guard the polygon, for each of the two triangulations.
f. What is the minimum number of vertex guards for each polygon?
g. What is the minimum number of guards (possibly in the interior) for each of the polygons?
h. What is the minimum number of convex pieces can you decompose each of the polygons into?
i. How many other vertices can vertex 4 of the first polygon see? How many vertices can vertex 5 see? (Remember that a vertex can always see its two neighbors along the polygon, because we are not requiring "clear vision.")
j. Are there non-convex polygons for which a single vertex can see all of the other vertices of the polygon?
k. How many vertices does the convex hull of the polygons below have?
l. Can you draw a simple polygon with 9 vertices but for which the convex hull has only 3 vertices?
