Review For Final Examination (Spring 2007)
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
http://york.cuny.edu/~malk
1. Draw a diagram of the following (when possible the diagram should be drawn in the plane):
a. A scalene right triangle
b. An equiangular triangle and an equiangular quadrilateral
c. An equiangular 4-gon that is not a square
d. An equilateral quadrilateral that is not a square
e. A non-convex, non-self-intersecting 4-gon
f. A trapezoid with three equal sides that is not a rectangle
g. An equiangular hexagon which is not a regular hexagon
h. A self-intersecting regular pentagon
i. An isosceles right triangle
j. An acute angle triangle
k. A parallelogram which is not a rectangle or a rhombus
l. A rhombus which is not a square
m. A quadrilateral with exactly two, nonadjacent right angles
n. Draw a graph with 10 vertices and 14 edges
o. Draw a simple polygon with exactly 3 ears
p. Draw an isosceles triangle which is not equilateral
q. A non-convex self-intersecting 7 sided polygon
r. Give some examples of 3-dimensional geometrical figures
s. Give some examples of 2-dimensional geometrical figures
t. What is the difference between a ray and a segment?
u. Draw graph which is planar but not plane.
v. Draw a 3-valent graph which is planar but not plane (e.g. all its vertices are 3-valent)
2. Give a precise statement of the graph theory version of Euler's formula.
3. Draw a graph to which one can not apply Euler's formula.
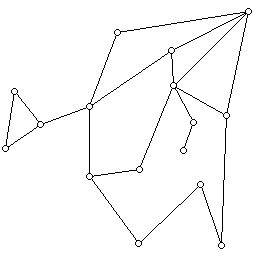
4. a. Write the pi values for the faces of the graph below.

b. Is there a pair of vertices u and v in the graph above such that there are three independent paths (e.g. only u and v in common) between these vertices?
c. Is the graph above 3-connected?
5. Draw an example of a 3-valent (e.g. every vertex is 3-valent) which is 3-polytopal. (G is 3-polytopal if it is the vertex-edge graph of a 3-dimensional polytope).
6. Draw an example of a 4-valent graph (e.g. every vertex is 4-valent) which is 3-polytopal.
7. Draw a plane graph with every vertex having valence at least 3 which is not 3-polytopal.
8. Give a statement of the four color conjecture.
9. Can one color the faces of the graph in Problem 4 above with exactly 3 colors?
10. For the polygon below:
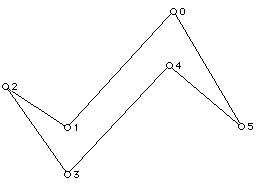
a. List all of the ears.
b. Draw the visibility polygon of vertices 4 and 2.
c. Determine the minimum number of guards to guard the polygon.
d. Draw two different triangulations of the polygon.
e. 3 color the vertices of the each of the triangulated polygons you obtain in d.
f. LIst all the reflex vertices of this polygon.
h. How many vertices does the convex hull of this polygon have?
11. Give a precise statement of Euler's Theorem for graphs. Draw a plane graph which when computes the Euler characteristic one does not get 2.
12. Can a polyomino have a perimeter of odd length? Can you prove this using mathematical induction? (To use induction you need to be able to show that for any polyomino with at least two cells that one can remove some cell to get a smaller polyomino.)
13. Draw two different nets for a triangular prism. (3-valent graph with three 4-gons and two 3-gons).
14. Briefly describe models for: affine geometry, projective geometry, and hyperbolic geometry in each of the finite and infinite situations.
14. The situations below concern the relation between the Euclidean and real-projective planes.
a. What projective points correspond (if any) to the Euclidean points: (-2, 4); (0, 3); (-9, 0)?
b. What Euclidean points correspond (if any) to the real projective points:
(-1, 2, 4); (0, 2, 1); (0, -3, 0); (-2, 5, 4); (-2, 0, 0).
c. Find the line that goes through (0, 3, 0) and (-2, 4, 2) in the real projective plane?
d. Find the line through goes through (-2, 4) and (2, 6) in the Euclidean plane.
e. Find the point if there is one where the lines 2x - 3y + 4 = 0 meets -x + 2y + 8 = 0 in the Euclidean plane.
f. Find the point where 2x - y + z = 0 and -x + y + 4z = 0 meet in the real projective plane.
g. Draw a diagram to illustrate Desargues Theorem in the real projective plane.
h. Are the lines x-y = 0, x +y -z = 0 and y = 0 concurrent?
i. Draw a diagram of the Fano plane.
j. If a finite affine plane is coordinatized with numbers from GF(7):
i. How many points will the geometry have?
j. Evaluate:
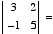

15. Find the Hamming distance between the sequences below:
a. 10111010 and 11110000
b. ACGTTTAGT and CAGTTAAGC
16. Given the points:
A = (-2, 4), B = (2, 6), C = (6, 2)
a. Find the taxicab distance length of the sides for this triangle.
b. Find the Euclidean distance length for the sides of this triangle.
c. What points are equidistant between B and C with respect to Euclidean distance?
d. What points are equidistant between B and C with respect taxicab distance?
e. What points are equidistant between B and A with respect to Euclidean distance?
f. What points are equidistant between A and B with respect taxicab distance?
g. What is the equation of a Euclidean circle center at B and radius 4?
h. Sketch a graph of the taxicab circle center at (6, 2) and radius 3. Draw at least 4 points on this circle.
17. Draw 5 inequivalent pentominoes?
18. A triangular prism is a polyhedron which is 3-valent and has 2 triangles and 3 squares.
a. Draw a plane graph which represents the triangular prism.
b. Draw a net for the triangular prism
c. Is the net of a triangular prism a polyomino? Explain.
19. Be able to write down the addition and multiplication tables for Z6 or Z7.
20. Know the parallelism axioms for an affine (Euclidean), projective and hyperbolic geometry.
21. Be able to draw diagrams for a finite affine, finite projective, and finite hyperbolic plane.
22. Be able to state Euclid's 5th Postulate from the Elements.
23. Draw graphs of the 5 regular (Platonic) solids.
24. Find the Hamming distance between pairs (this requires 6 calculations) of binary sequences below:
A = 00000000
B = 00011111
C = 11111000
D = 11100011
25. Draw a picture of the Cayley-Klein model for the hyperbolic plane. What are the points of this model? What are the lines of this model?
26. When the sphere is thought of a projective geometry what are the points and the lines of the geometry?
27. Know the statement of the Klee-Chvatal Art Gallery Theorem.