
Combinatorial and Discrete Geometry: Sheet M (Matchings)
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk
Definitions
1. If G is a graph a matching M is a collection of disjoint edges of G. (Two edges are disjoint if they have no vertex in common.)
2. If M is a matching of G, M is said to be a maximum cardinality matching if no matching of G has more edges than M.
3. If M is a matching of G, M is said to be a maximal matching if no edge of G can be added to M and still be a matching.
4. A matching M of G is said to be perfect if every vertex of G is a vertex of some edge in the matching.
For each graph below:
a. If possible find a matching with 4 edges.
b. If possible find a maximal matching with 3 edges.
c. If possible find a perfect matching.
d. Find a maximum cardinality m
G:

H:
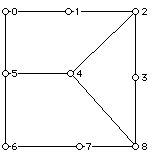
I:
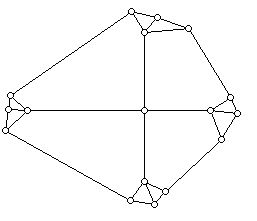
J:

K:

L:
