Combinatorial and Discrete Geometry: Sheet J

Prepared by:

Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451

email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk

Definition:

A Hamiltonian cycle (HC) in a graph is a cycle which passes through all of the vertices of a graph once and only once. (Note: A Hamiltonian cycle can be thought of as starting at any of its vertices.)

For each graph below determine if the graph has an HC, and if it does write one down. If not try to give a reason why the graph has no HC.

1.

2.

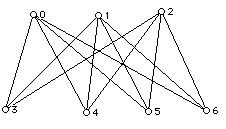
3.

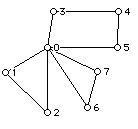
4.

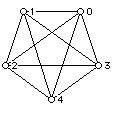
5.

6. (Petersen graph)

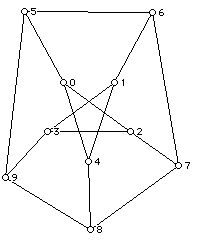
A graph has a Hamiltonian path if it has an open trail that includes all of the vertices of the graph. A graph is called Hamiltonian connected if it has a Hamiltonian path between every pair of its vertices. Do the graphs above have Hamiltonian paths? Are any of them Hamiltonian connected?