Mathematics 243 (Combinatorial and Discrete Geometry)

Review: Examination II

prepared by:

Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451

email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk

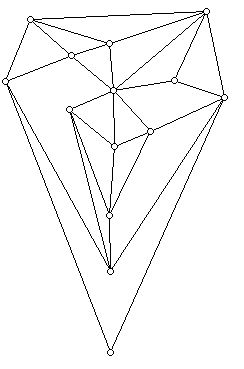
1. a. Draw a tree whose only vertices are 1-valent and 5-valent, and has 3-valent vertices. How many edges does this tree have?

b. Draw a tree which has vertices of valence 1, 3, 5, and 7 and no vertices of other valences.

c. Some of the properties of a graph that must hold if the graph is a tree but will not hold if the graph is not a tree.

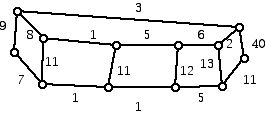
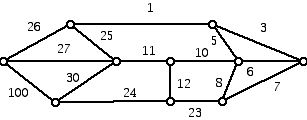
2. For the graphs below use:

a. Kruskal

b. Prim

c. Boruvka (use this method only when the edges all have different weights)

to find a minimum cost spanning tree for the graph as well as the cost associated with that tree:

3. Draw a connected weighted graph G which has cycles and for which the two most expensive edges in G are present in any minimum cost spanning tree for G.

4. Give some examples of real world situations where the finding a minimum cost spanning tree would be required.

5. For each graph below give if possible a proper 3-coloring of the graph, and determine the vertex chromatic number of the graph and give a proper coloring that uses the chromatic number of colors:

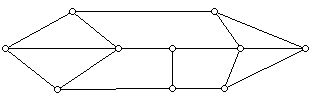
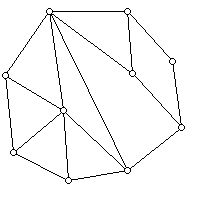
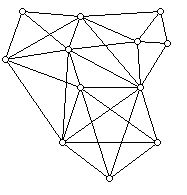
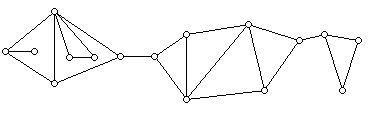
6. For each graph in Problem 5 which is a plane graph, wrote down the degree sequence of the graph and the face vector of the graph. (The face vector records the values p_i which give the number of faces of the graph which have i sides.)

7. Draw a planar graph with 6 vertices which is bipartite, connected, has a cycle of length 5, and is not a plane graph.

8. For each graph below:

a. If possible find a matching with 5 edges.

b. If possible find a maximal matching with 5 edges.

c. If possible find a perfect matching.

d. Find a maximum cardinality M