
Theorem: If T is a tree with n vertices then T has (n-1) edges.
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
email: joeyc@cunyvm.cuny.edu
The theorem of the title:
If T is a tree with n vertices then T has (n-1) edges
can be proved using mathematical induction.
Before starting the proof, recall some basic graph theory definitions and facts:
1. Definition: A tree is a connected graph which has no cycles.
2. Theorem: If T is a tree different from K1 (i.e. not a single dot), then T has at least two vertices which have degree 1 (i.e. 1-valent).
Let s(n) be the statement: A tree with T with n vertices has (n-1) edges.
s(1) requires that a tree with 1 vertex has 0 edges. There is only one such graph, a graph with a single dot. This has no edges. Therefore, s(1) is a true statement
Note that s(2) also is true. S(2) states that a tree with two vertices has one 1 edge. There is only one such tree, K1 (a pair of vertices jointed by an edge) which has 1 edge.
We will now assume that s(k) is true.
Namely, if T is a tree with k vertices then T has k-1 edges.
Now, let T* be any tree with k+1 vertices (k greater than or equal to 1). We know that T*, since it has at least 2 vertices, has a vertex, call it w, of degree 1. (The one edge at w has another vertex v, which is part of the tree.)
(Although the argument being given does not depend on a diagram many of you may like to refer to the diagram below, which represents T*.)

Now let T=T*-w, the graph obtained from T* by deleting the vertex w. T has no cycles, is connected, and, thus, is a tree with one less vertex than T*, namely, k vertices. Now using the italicized statement above (known as the inductive or induction hypothesis) we conclude, since T has k vertices that it has k-1 edges. (Below is the picture of T for the case where T* is the tree above.)
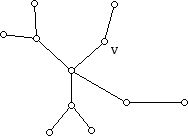
What does this tell us about T*? To get from T back to T* we have to put back the edge we removed, the edge vw. Thus, T* has exactly one more edge than T, and since T has k-1 edges we conclude that T* must have k edges. Thus, we have shown (using the inductive hypothesis) that any tree of k+1 vertices has k edges. Thus s(k) was used to prove s(k+1).
Hence, we can conclude using the Principle of Mathematical Induction that s(n) is true for all values of n.
Remember what the Principle of Mathematical Induction says is:
a. if s(n0) is true
and
b. if s(k) implies s(k+1) (for k greater than or equal to n0)
then
s(n) is true for all n.