Discrete Mathematical Structures; Mathematics 225

Review Examination III (Spring 2005)

Prepared by:

Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451

joeyc@cunyvm.cuny.edu

web page:

http://www.york.cuny.edu/~malk

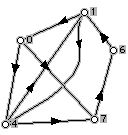
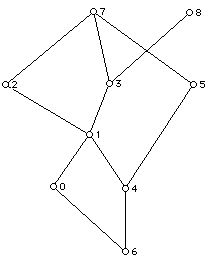
1. Given the digraph below:

a. Write down the relation associated with this digraph.

b. Write down the invalence and outvalence (also known as indegree and outdegree) of each vertex of the digraph.

c. Write down the adjacency matrix associated with this digraph.

d. Find, if possible, a path of length three starting at vertex 0.

d. Find, if possible, a cycle of length 2.

e. Find if possible a cycle of length 4.

f. Find the number of vertices in the digraph.

g. Find the number of edges in the digraph.

2. Is f(n) = 3n² + log n + 9

a. O (n³) b. O ( 2ⁿ ) c. O ( n ) d. O ( n² )

3. Compute f(2), f(-3), f(0), and f(1/2) for the functions:

a. f(x) = 3x - 5

b. f(x) = 4^x

c. f(x) = -x² + 4x - 1

4. Suppose g(x) = 2x - 3, and h (x ) = 2^x

a. Find g (h(2)) and h(g(2).

b. Fine h(g(3)) and g(h(3))

c. Find h(g(-1)) and g(h(-1)).

5. Suppose the domain of g(x) = x² is all real numbers and its codomain is are real numbers which are at least equal to -1. Is this an onto function? (Explain.) Is this a 1 to 1 function? (Explain.)

5. Given the Hasse diagrams below for a poset (partially ordered set):


a.

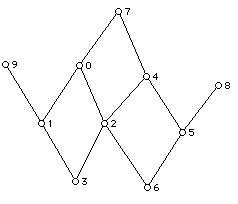
b.

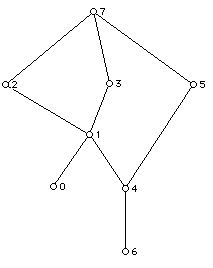
c.

i. Find all the maximal and minimal elements in each Hasse diagram, if there are any. Find a greatest element and a least element in each Hasse diagram if they exist.

ii. Conduct a topological sort for each of the Hasse diagrams. Is the linear order you obtain unique?

iii. Draw the full partial order associated with the Hasse diagram c. above.

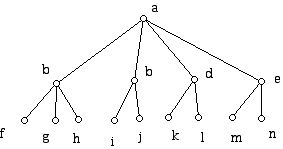
6. Consider the graph G below:

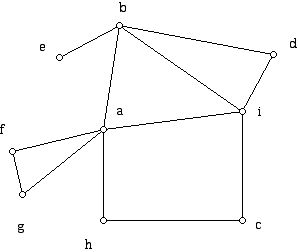
a. Determine the number of vertices of G

b. Determine the number of edges of G

c. What is the valence of each vertex of G?

d. Can you find a path of length 2 from f to i?

e. Can you find a path of length 5 from f to i?

f. What is the graph distance from e to each of the other vertices in the graph?

g. What is the graph distance between c and every other vertex of the graph?

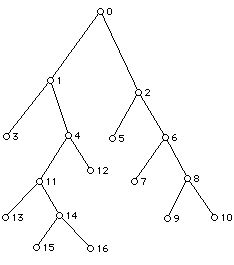
7. Write down the list of vertices which results from

a. Postorder
b. Preorder

c. Inorder

traversal of the trees below:



Tree S:

Tree T:

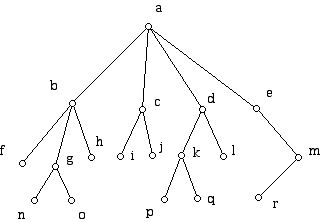
Tree W: