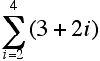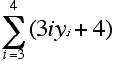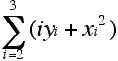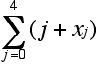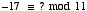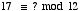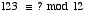Review For Final Examination (Spring, 2007)
Mathematics 225 (Discrete Mathematics)
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
1. Write down the truth tables for: and, or, implies, if and only if, and not.
Know how to check expressions to see if they are tautologies or contradictions:
Is:

a tautology.
2. The Universe class below represents American women over 21:
A = those who have developed breast cancer
B = those who work part time
C = those who are college educated
(Note: The complement of X is indicated by X '.)
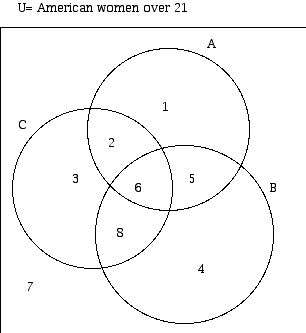
a. Which region(s) represents 
b. Which regions represent: 
c. Give a verbal description of region 8.
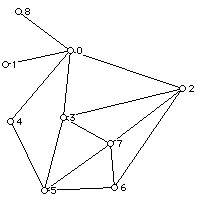
d. Give a verbal description of regions 2 and 6 as a group.
e. Give a symbolic description of regions 2,3, 6, and 8 collectively.
f. Give a symbolic description of region 7.
g. Which region (s) are represented by (A union B) intersect C '.
3. Given: x1 = -2, x2 = 4, x3 = 0, x4 = -2, and x5 = -1
and y1 = -3, y2 = -4, y3 = 6, y4 = 0, and y5 = 2.
a. Compute:
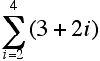
b.
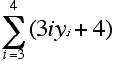
c.

d.
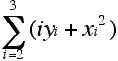
e.

4. Re-index the sum below so that it starts at j = 3:
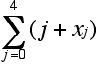
5. Suppose that U = { a, e, i, o, u, y, z }
and A = { a, e, i, y }, B = { i, e, o } and C = { i, u, y }
a. A ‹ B
b. A ' ‹ C ' › B
c. B › C '
d. (B › C ' ) ' ‹ A
6.
a. How many binary sequences of length 8 are possible?
b. How many binary sequences of length 8 are there that begin and end with two 0's?
c. How many binary sequences of length 8 are there have ones in odd numbered positions?
7. Compute:
a. 4!
b. 6! - 3!
c. 10P4
d. 19C3
e. 76C73
8.
A Congressional committee has 5 women Republicans, 2 women Democrats, 5 male Republicans and 6 male Democrats.
a. How many ways are there to chose a chairperson and a vice chairperson?
b. How many ways are there to choose a subcommittee of 5 members?
c. How many ways are there to choose a subcommittee of 5 members that include no women?
d. How many ways are there to choose a subcommittee of 5 members who are all Democrats?
e. How many ways are there to choose a subcommittee of 5 members who are all women or all Democrats?
9. Passwords are formed from decimal digits and letters, where the letters can be upper or lower case:
a. How many passwords of length 3 are possible if repeats are allowed?
b. How many passwords of length 3 are possible if repeats are not allowed?
c. How many passwords of length 4 are possible if the digit 1 can not be used to start or end the password?
d. How many passwords of length 4 are possible if all the symbols used are identical?
10. Find the least common multiple and greatest common division of:
a. 48, 120
b. 420, 98
by
i. Using prime factorization.
ii. Euclidean algorithm.
11. Find the quotient and remainder when:
a. 133 is divided by 65
b. -135 is divided by 10
c. -47 is divided by 3
d. 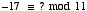
e. 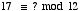
f. 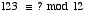
g. Find the value of x which solves the congruence: 7x congruent to 1 modulo 23
h. Find the vallue of x that solves the congruence 3x congruent to 1 mod 16
11. Find the inorder, postorder, and preorder traversal of the tree below:
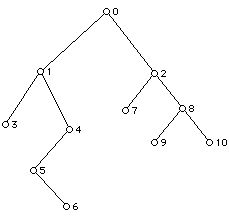
12. a. If f(n) = 200 log n + 4n
b. If g(n) = 1000000n + n log n + 5n
Determine if these functions are:
i. O(n) ii. O(2n) iii O(n5) iv. O(3n)
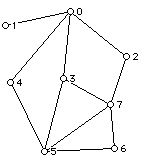
13. Construct a depth first search tree and a breadth first search tree starting at vertex 3. Repeat for vertex 6.
i.
b.
14. a. Find the distances between the vertex 4 and every other vertex for the graphs in 13.
b. In each graph write down all the cycles of length 5.
15. a. Find the minimal, maximal, least, and greatest elements in the Hasse diagram below if such elements exist.
b. Write down the valences of all of the vertices in the graph below if the diagram is interpreted as an undirected graph.
c. Is the undirected graph below a tree? If not, what is the smallest number of edges that must be removed to obtain a tree?
d. Is the pair (7, 2) an element of the associated partial order? What about the pair (0, 2) and (6,3)?
e. Find three different sets of incomparable elements of size 2.
f. Is there a set of incomparable elements of size 3?
g.. Perform a topological sort on this Hasse diagram.

16. Perform the indicated computations:
a, (101111)2 = (?)10
b. (272)10 = (?)2
c. (332)4 = (?)10
d. (101)10 = (?)2
e. (332)5 = (?)10
f. (101)6 = (?)2 (Be careful)
17. Write down the matrix associated with the digraph below:

b. Draw the matrix associated with the digraph shown.
c. If this digraph has any cycles write them down.
d. If there is a path from 4 to 3 write it down.
e. Is there a path from vertex 2 that has length 3?
17. Given f(x) = -x2 and h(x) = -x3
a. f o h (-2) = ? d. h o f (3) = ?
18. Write down the Hasse diagram for the partial order which gives the divisibility relation for the set of integers: { 3, 5, 10, 21, 14, 24, 28, 8, 7, 12}
19. Write down the symbolism which is used to represent:
a. For all x and for all y b. There exists a z such that for all y.
20. Find x and y (integers) such that: 27x + 16 y = 1.
21. Write down the multiplication and addition tables for Z5.
22. Construct a Huffman code and a Huffman tree for an alphabet with the following frequencies:
A = 2, B = 33, C = 100, D = 6, E = 14, F = 77, G = 22, H = 3.
How many bits are saved by using a Huffman code rather than a code with fixed length code words?