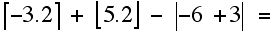Mathematics 225 (Discrete Mathematics)
prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, New York 11451
email: malkevitch@york.cuny.edu
1. Compute:
a.

b.
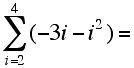
c.

2. Suppose x1 = -2, x2 = -1, x3 = 1, and x4 = 5 and y1 = 2, y2 = -2, y3 = 0, and y4 = 2.
Compute:
a.
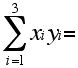
b.
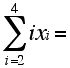
c.
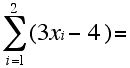
d.
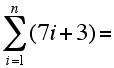
e.
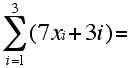
3. Prove using mathematical induction that for all n:

4. For each of the difference equations below determine the values of a3, and a4 assuming that a0 = -1.
a. an+1 = 5an + 2n + 5.
b. an+1 = -2an + n - 3
c. an+1 = -3an + 2(4n).
5. Solve the recursions below assuming that a0 = -4:
a. an+1 = -4an
b. an = 3an-1
6. Solve the recursion below assuming a0 = +3, a1 = -1
an+2 = -4an+1 - 3an
7. Determine if the following are tautologies. If not (if possible) give one set of truth for which the logical expression is true.
a.
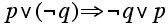
b.
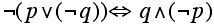
c.

d.

8. Compute:
a. 3! -5!
b. 5!
c. 6P3
d. 17C3
e. 76C73
9. An ice cream parlor offers sundaes with 6 types of syrup, 4 toppings, and 24 flavors of ice cream. How many different kinds of sundaes can be made?
10. a. How many binary sequences of length 7 are possible?
b. How many binary sequences of length 7 are there that begin and end with 10?
c. How many binary sequences of length 7 are there have ones in odd numbered positions?
d. How many binary sequences of length 7 are there that begin with two ones and end with a 0?
e. How many binary sequences of length 7 are there that begin with two ones or end with 00? (Be careful.)
11. Give an example of a proposition which is:
a. True
b. False
c. Truth status is not known.
12. The psychology club of a college has 11 members, 7 men.
a. How many ways are there to elect a president, a vice-president, and a treasurer for the club?
b. How many ways are there to elect a president, a vice-president, and a treasurer for the club if the president must be a girl?
c. How many ways are there to elect a president, a vice-president, and a treasurer for the club, if the vice-president and treasurer must be boys?
d. How many ways can a committee of 4 be chosen to interview the President of their college?
e. How many ways can a committee of 5 which has exactly 2 women be chosen?
f. How many ways can a committee of 4 be chosen if Mary must be on the committee?
g. How many ways can a committee of 5 be chosen in Mary and John must be on the committee?
h. How many ways are there to choose a committee of 5 if there can be at most one woman on the committee?
13. If the following result is true, prove it using mathematical induction:
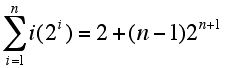
14. Suppose g(x) = 2x - 3, and h (x ) = 2x
a. Find g (h(2)) and h(g(2).
b. Fine h(g(3)) and g(h(3))
c. Find h(g(-1)) and g(h(-1)).
15. a. Write down the relation associated with the digraph below: