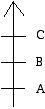
Fairness and Equity: Notes 11
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
More about elections.
So far we have developed a large number of election systems where each system was designed so as to be appealing from some perspective. On this basis we can design, using ordinal ballots, plurality voting, run-off, sequential run-off (IRV, recently adopted in San Francisco for municipal elections), the Borda Count, Condorcet, Coombs, or Nanson. (Nanson's method is to use a run-off based on the Borda Count. Somewhat amazingly, this system will always produce the same person as winner as the Condorcet method when there is a Condorcet winner. When there is no Condorcet winner, however, the method does select one of the candidates to win the election.) How can one tell which of these methods is better than another?
It was this challenge which was taken on by Kenneth Arrow. Arrow was educated at City College in New York City, before City College became one of the units of City University of New York (CUNY). After graduating from City College Arrow attended Columbia University where he studied economics. In his doctoral thesis he developed the ideas about voting systems and decision making systems which involved how society could reach decisions based on the input of a collection of "voters" or decision makers. This work later won him the Nobel Memorial Prize in Economics. (Alfred Nobel did not create a prize for work in Economics. Later, in his memory, additional money was made available to create a new prize, the Nobel Memorial Prize in Economics.)
Arrow's simple but brilliant idea was to ask: What are the properties that one wants a good voting, or fair voting system to obey?
In the original framework that Arrow developed each voter provided a ranking, with ties (indifference) allowed between candidates. These ballots were submitted to a decision making group ("board of elections") who used some system previously decided upon in advance as to how to choose a ranking for society. (In most elections we are familiar with a single winner is chosen from the alternatives, however, Arrow considered the case where the board of elections chose a ranking (indifference allowed) involving all the alternatives for society. (More recently, scholars have extended his work to the case of a single winner, the result being the same conclusion as was the case for Arrow's original work.)
Arrow first pointed out that one method of translating voter preferences into a societal choice was to have the decision for society always agree with the ballot of one particular voter. In this system, one voter gets his/her way, and this is the system we would call a dictatorship. In a dictatorship society follows the lead of the dictator.
Arrow also insisted that the election board choose some ranking, no matter how "irrational" the votes of the voters might appear. This rule means that one can not use the Condorcet method in its "vanilla" form, since this method will not always produce a top ranked alternative, that is, an alternative that can beat every other alternative in a two-way race. This condition is known as the decisiveness condition.
Arrow also noted that there are situations where decisions are made without consulting the ballots, so called "imposed systems." To give you the idea of what is involved here, in ancient Greece legend has it that if an important decision was to be made, often instead of making the decision himself a leader could go to the Delphi oracle who would give "advice" on what to do. If the board of elections were to go to an oracle instead of following some rule that "consulted" the ballots, this would be an imposed system. Arrow pointed out that an imposed winner would not be consistent with democracy.
One can think of these three conditions above as being examples of "fairness conditions." One can also imagine conditions on an election system which in order to be be fair would involve "being consistent."
The monotonicity condition is an example of such a condition.
Consider two elections which are identical except for the way one voter cast his/her vote. (All the ballots except for those of one voter Q are the same in the two elections.)
In election I, this voter Q produced the ballot below:
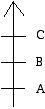
while in election II, this voter Q produced the ballot:
Suppose Method M was used in both of these two elections. Suppose in Election I, method M selected A as the winner, while in election II, B was the winner. What would you think of Method M?
Since in Election II candidate A did better on one ballot and B did worse on one ballot (all the other ballots being the same in the two elections) one would reason that Method M was flawed! It should have elected A in election II if it elected A in election I because A put in a stronger showing in election II. A should not be penalized for "doing better!"
An election system which violates this condition, that when a candidate gets more support it hurts the candidate is called a violation of monotonicity. If you think monotonicity is an essential feature of an election system then you can not endorse the use of IRV, because IRV violates this condition!
Arrow also, in his work described the idea of the Independence of Irrelevant Alternatives. This condition is again a consistency condition. It says that the relative ranking of two alternatives A and B should depend only on A and B and not how A and B are ranked when compared with some additional alternative C.
If one thinks that the independence of irrelevant alternatives is critical for a fair election method, then one can not employ the Borda Count, since this method violates this fairness rule.
So what method did Arrow endorse as the fairest method for conducting elections? Here is what Arrow demonstrated:
Suppose one has an election with 3 or more candidates, which is decisive in the sense that it always produces a ranking. Then, there is no election method which meets all of the conditions listed above!!!
Arrow's Theorem means that when using ordinal ballots to decide an election with 3 or more alternatives there is no perfect method of deciding the election. It does not mean that we should be content with plurality because there is no perfect method. Arrow's theorem means that one can not have "everything" that one might want.
One way to think of Arrow's Theorem is that it helps explain why there is so much "anger" centered around how to resolve fairness problems. Group A will argue that the important conditions to meet are x, y, and z, while a different group will argue that the important conditions to meet are u, v, and w (some of which may be the same as x, y, and z). These two groups will fight to get its way. A "mediator" might suggest one use a method that meets all of the conditions. Arrow's Theorem says that for elections with 3 or more alternatives this will not be possible! So the groups are doomed to feud about which fairness conditions are the truly essential ones.
One final word about elections. We all know that one way to get ahead in the world is to sometimes stretch the truth, or tell a lie. If someone asks when you apply for a job whether or not you have experience you can tell them that you do, when, in fact, this is not so. This raises the question, suppose you know what system the board of elections is using to decide an election. Can you use this information to get a more favorable outcome for yourself? A result related to Arrow's Theorem, again proved by two economists, A Gibbard, and M. Satterthwaite deals with this question. They show that where there are three or more candidates for elections with ordinal ballots, that regardless of what method is used, there will always be situations in which it pays to "lie" about one's true preferences because it will give one a better over-all result to lie!
Like Arrow's Theorem, this result, too, is deeply disturbing. One way to think about what should be done is to use a method that does not make it easy to manipulate the system. Some people for example think that this is a big strike against the Borda Count. For example, if your true preferences are A best, and B next best, if you rank B last instead of second, this will increase the chance that your first choice A will win, because by voting for B in second place you may help B to win, while by ranking B last, A will do better, relatively. Of course, those voters who rank B first may also lie about there feelings about A. It would be nice if there were a voting method which would reward truthfulness but this is not possible. This is one reason that many people are opposed to information voter preferences being published before an elections. If I know what other voters will actually do, I can lie about what my preferences are to help get a desired outcome.