Euler's Combinatorial and Geometrical Mathematics: Problem Set I
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Rules: You can consult print sources as you wish and you can work together with other students if you like provided that you write up your solutions on your own. You can submit you solutions either hand written or using a word processor. Diagrams are encouraged and should be done either by hand, or using software. Those who use MAC computers will find the freeware Cabrigraph useful for drawing graphs. If working on these questions suggest any conjectures, include them in your work. Please start each new problem on a new sheet of paper.
1. Construct examples (with proof) of 3-polytopal graphs which have no Hamiltonian Circuit based on the ideas of Grinberg's Theorem which are:
a. 3-valent
b. has a least one vertex which is 4-valent
c. has at least one vertex which is 5-valent
2. Prove or disprove:
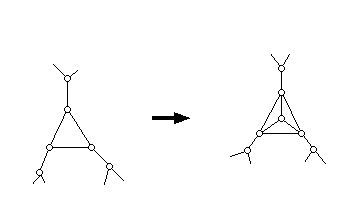
If G is a plane triangulation (e.g. every face has 3 sides) with at least 4 vertices then if a pyramid is erected on each face, the resulting graph has no hamiltonian circuit.
Note: a. If the statement is false can you find an infinite family of graphs for which it is false. b. If it is false can you find a way of modifying the statement so that it becomes true, and prove your modified version.
Note: b. The diagram below shows the process of erecting a pyramid on a single face of a graph which is a 3-gon. This process can be carried out for faces that are not necessarily triangles by joining a vertex in the interior of a face to all of the vertices of that face using edges.)

3. Given the graph H below:

a. Write down the degree (valence) sequence of the graph H.
b. Write down the face vector of the graph H below.
c. Prove or disprove that H has a hamiltonian circuit. If H has no HC can you use Grinberg's Theorem to show this?
4. A graph G is called a Halin graph it arises from a tree embedded in the plane which has no vertices of valence 2 by passing a simple circuit through the 1-valent vertices of the tree. An example is shown below, where the added circuit is shown with thick edges.
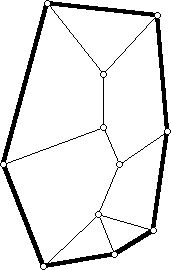
a. Prove or disprove that Halin graphs are 3-polytopal.
b. Prove or disprove that a Halin graph always has a face which is a 3-gon.
c. Prove or disprove that Halin graphs always have a Hamiltonian circuit.
d. Prove or disprove that Halin graphs always of circuits of all lengths.
e. Prove or disprove there is some Halin graph H with all its vertices having valence 3 such that for any positive integer m (which is at least 4), there is a face with m sides in H.
f. Can you find a Halin graph which is 3-valent whose medial graph does not have a cut-through Eulerian circuit? If it does not have a cut-through Eulerian circuit, must it have a cut-through simple circuit?
g. Can you find a Halin graph which is not 3-valent whose medial graph does not have a cut-through Eulerian circuit?
5. If a plane graph 3-connected graph G has V, F, and E vertices, faces, and edges, respectively, can you determine the number of vertices, edges, and faces of the medial graph of G in terms of V, F, and E? How are valence vector and face vector of G related to the medial graph of G?
Definition:
A tree is called a k-tree if its vertices which are not leaves are k-valent.
5. If a k-tree, T(n, k), has n vertices which are k-valent, what can you say about the number of vertices that T(n, k) must have?
---------------------------------------------------------------------------------------------------------------
If during your work on these problems, questions occur to you that you think it might be interesting to answer, please submit these questions along with your solutions.