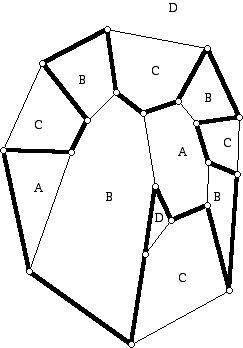
Figure 1 (A Hamiltonian circuit for which the faces in its interior have been colored with A and B and faces in its exterior have been colored with C and D so that the resulting coloring is a 4 coloring of the faces of the graph.)
Hamiltonian Circuits in Plane Graphs
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Attempts to prove the Four Color Conjecture (now the Four Color Theorem), which asked if every plane graph could be face colored with 4 or few colors, resulted in considerable interest in whether or not plane 3-valent 3-connected graphs have Hamiltonian circuits. The question of whether or not a plane graph can be 4 face colored can be reduced to the question of whether or not a 3-valent, 3-connected (hence, 3-polytopal) plane graph can be 4 face colored. It is easy to see, as was observed by Hassler Whitney, that any plane graph (whatever its valences might be) which has a Hamiltonian circuit can be 4 face colored. The idea for how to show this in general is illustrated via the diagram in Figure 1. The edges which are not part of the Hamiltonian circuit either appear in the interior of the Hamiltonian circuit C or its exterior. The interior diagonals have the property that faces on opposite sides of any (interior) diagonal have to have different colors. So, one chooses any region in the interior, and colors it, say, A. Now every time one crosses an interior diagonal one changes the color between A, and a second color B, but all one needs for the interior faces are these two colors. Similarly, one can alternately color the faces in the exterior of the Hamiltonian circuit C and D.

Note that it may well be possible to face color the plane graph with fewer than 4 colors, but we are not looking for the value of the chromatic number (minimal number of face colors) for the particular graph, only for a guarantee that it can be colored with 4 or fewer colors.
For a long time it appeared that it might be true that plane 3-valent 3-connected graphs might all have hamiltonian circuits. Part of the problem is that the number of vertices in a smallest counterexample we now know has 38 vertices. However, William Tutte, in 1946, was the first to construct a a 3-valent, 3-polytopal graph which lacks an HC.
For a long time it appeared to be hard to come by examples of non-hamiltonian 3-valent 3-polytopal graphs. However, in 1968, a surprisingly simple but clever argument made it possible to construct examples of such graphs relatively easily. This argument was provided by the Latvian mathematician Emanuel Grinberg in 1968. Easy constructions of non-hamiltonian graphs follows from the use of the formula:
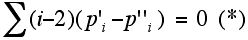
Here, p'i denotes the number of faces with i sides in the interior of a HC in a plane graph and p''i the number of faces with i sides in the exterior of the HC.
To clarify the notation in (*) and how the proof goes, examine the diagram in Figure 2.
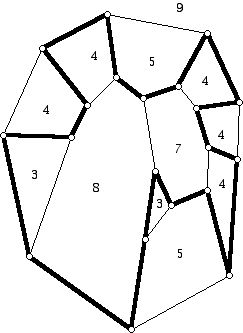
We start with our graph embedded in the plane and an HC indicated. For the example above we have:
| value of i | p'i | p''i |
| 3 | 1 | 1 |
| 4 | 3 | 2 |
| 5 | 0 | 2 |
| 6 | 0 | 0 |
| 7 | 1 | 0 |
| 8 | 1 | 0 |
| 9 | 0 | 1 |
Substituting in (*) we have:
(3-2)(1-1)+(4-2)(3-2)+(5-2)(0-2)+(6-2)(0-0)+(7-2)(1-0)+(8-2)(1-0)+(9-2)(0-1)=
0-2-6+0+6+6-7 = 0 as required if Grinberg's equation holds.
Let us denote by n the number of vertices in our plane graph. Furthermore let the number of edges that are interior to the hamiltonian circuit, the "interior chords" or "interior diagonals" of the circuit be denoted by di. Similarly, de will denote the number of edges that are exterior to the hamiltonian circuit, the "exterior chords" or "exterior diagonals."
Note that interior diagonals are edges of two interior faces, while the exterior diagonals are edges of two exterior faces. Furthermore, the edges of the hamiltonian circuit, which are the same in number as the number of the vertices of the graph (since the vertices lie on a hamiltonian circuit) touch one interior face and one exterior face.
These observations allow us to see that if we weight the number of interior faces with i sides by i we get the number of vertices in the graph plus the number of diagonals counted twice, and similarly for the exterior faces.
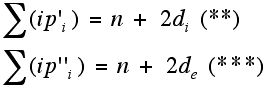
Subtracting we get that:
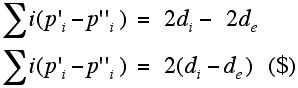
However, the number of interior faces is given by 1 + di and the number of exterior faces is given by 1 + de.
Hence, we have:

When we substitute these in ($) we get:
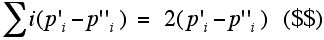
which simplifies to the Grinberg equation (*)!
The way that the Grinberg equation is applied are varied but the most straightforward is to construct a plane graph which has faces all of which have a number of sides congruent to 2 mod 3, except for one face S. Since the faces S must be interior to or exterior to any HC in such a graph the Grinberg equation gives rise to a contraction, when looked at modulo 3. All the faces which have a number of sides such as 5, 8, 11, etc. give rise to zero terms mod 3, while the face S contributes (|S| -2) with either a positive or negative sign.
There are a variety of other things to notice here.
a. If a 3-valent graph has a hamiltonian circuit C, the edges not in the circuit C form a perfect matching of the graph. A perfect matching is a collection of disjoint edges which includes all of the vertices of the graph.
b. If a 3-valent graph has an HC then the edges of the graph can be edge colored with 3 colors. This is done by alternately coloring the edges of the HC with, say, the colors a and b. Now the remaining edges of the graph, those which constitute a perfect matching can be colored with a third color.
There are still many areas of investigation on the interface between colorings, hamiltonian circuits, and polyhedra.
One simple to state problem which is still open is:
(David Barnette)
Does every plane, 3-valent, 3-connected, bipartite graph have a hamiltonian circuit?
If any of the words above are omitted the statement fails to be true.
References:
Grinberg, E., Plane homogeneous graphs of degree three without hamiltonian circuits, Latvian Math. Yearbook, 5 (1968) 51-58.
Tutte, W. T. "On Hamiltonian Circuits." J. London Math. Soc. 21, 98-101, 1946.