Mathematics 483 (Game Theory)
Review: Midterm Examination
prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451
email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk
1. The game below is a zero-sum game with two players Row and Column where the payoffs are given from Row's point of view:
| I | II | III | IV | |
| 1 | 2 | -3 | 4 | 6 |
| 2 | 7 | 2 | -3 | 4 |
| 3 | 2 | 1 | -7 | 5 |
| 4 | 5 | 0 | 0 | 1 |
a. What is the payoff to Column if Row plays 3 and Column plays III?
b. What is the payoff to Row if Row plays 2 and Column plays IV?
c. What is Row's best/worst action?
d. What is Column's best/worst action?
e. Simplify the game matrix above by determining if any rows or columns dominate other rows and columns. Is there a single value for this game in pure strategies?
f. Write down a matrix would represent the payoffs for the game above from Column's point of view?
2. Determine the value of the zero-sum games below. In each case state if the value of the game is in pure-strategies or in mixed strategies:
a.
| Column I | Column II | |
| Row 1 | 2 | 0 |
| Row 2 | 4 | -1 |
b.
| Column I | Column II | |
| Row 1 | 5 | 1 |
| Row 2 | 3 | 2 |
c.
| Column I | Column II | |
| Row 1 | -5 | 2 |
| Row 2 | 6 | -3 |
d.
| Column I | Column II | |
| Row 1 | 2 | -4 |
| Row 2 | -4 | 8 |
In conjunction with solving the above problems:
i. Give the value
ii. State whether or not the value arises from using pure or mixed strategies.
iii. Draw, for the case where mixed strategies are required, the "spinner" which yields for each player the optimal solution.
3. Explain why for the game below, if Row plays Row 1 and 2 using any deterministic pattern that Row will not have an expected value of 0 in the long term:
|
Column I |
Column II | |
| Row 1 | -4 | 4 |
| Row 2 | 4 | -4 |
4. For the games below determine if there are any equilibria in pure strategies, and draw a "motion diagram" for the game. Also, record the payoff to Row and Column when 1 is played by Row and II by Column. What is the best/worst outcome and actions for each of Row and Column.
a.
| Column I | Column II | Column III | |
| Row 1 | (-1, 6) | (1, -2) | (5, -4) |
| Row 2 | (3, 0) | (2, --1) | (4, 3) |
| Row 3 | (4, 4) | (0, 0) | (3, -1) |
b.
| Column I | Column II | Column III | |
| Row 1 | (-1, -3) | (1, -1) | (-1, 5) |
| Row 2 | (3, -3) | (2, 12) | (4, -4) |
| Row 3 | (-2, -4) | (0, 0) | (-1, 1) |
c.
| Column I | Column II | |
| Row 1 | (10, -6) | (-2, 9) |
| Row 2 | (-5, 2) | (1, -3) |
5. Find any equilibria in pure strategies that might exist for the game below, and if there are no such equilibria find a Nash Equilibrium in mixed strategies. (Draw the motion diagram.)
| Column I | Column II | |
| Row 1 | (4, -6) | (-3, 4) |
| Row 2 | (-3, 4) | (2, -2) |
What is the best/worst action for each player above?
What is the payoff to Row and Column when Row plays 1 and Column plays I?
6. Which action would be taken in the game against Nature below, if Row uses:
a. Best/worst
b. Maximizes expected utility where each state of Nature occurs with equal probability.
c. Minimizes the maximal regret
| I | II | III | |
| Row 1 | -16 | 2 | 50 |
| Row 2 | 6 | -3 | 12 |
| Row 3 | 11 | 0 | -5 |
| Row 4 | 8 | -3 | -12 |
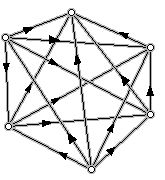
7. In the diagram below, an arrow from one vertex to another means that the outcome at the head of the arrow is preferred to the outcome at the tail. Label the dots of this "directed graph" (e.g. digraph), using the numbers 10 to 16, so that if one outcome is preferred to another then the label is a bigger number.
Comment: Diagrams of this type, where one has a collection of dots and directed line segments between them are often called tournaments. The reason is that one can think of the dots as players in a tournament, and when player i beats player j in a game one draws a directed line segment from i to j. For preference structures one can not have a cycle in such a graph but in ordinary tournament graphs, cycles are not uncommon.)

8. Consider the game below:
| Column I | Column II | |
| Row 1 | (14, 14) | (-20, 40) |
| Row 2 | (40, -20) | (-2, -2) |
a. Draw a motion diagram for this game.
b. What is the "rational" way to play this game i. once ii. many times assuming assuming that one is not allowed to consult with one's opponent?
c. Why might one expect that playing Row 1 and Column I by Row and Column will be sometimes not be the observed behavior one sees when this game is played?
9. Write down a symmetric game matrix for "chicken" where one uses the payoffs 4, 3, 2, 1 for each player (4 most preferred). (Hint: Chicken is similar to the Prisoner's dilemma, which appears above, except that there are no dominating rows and columns.)