Review: Examination I
prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451
Email: malkevitch@york.cuny.edu
web page: http://www.york.cuny.edu/~malk
1. Determine the value(s) of x for which the following equations and inequalities are satisfied. (If the solution set is an interval or ray, write down the solution in interval notation.)
a. x = 7
b. -x = 3
c. 2x = 16
d. 9x = 36
e. -x = 13
f. -5x = 35
g. 13x = 15
h. x + 11 = -2
i. 3x - 5 = 7
j. 2x + 12 = -6 + 3x
k. 5(x - 2) = 2x - 40
l. x > 12
m. 2x -8 < x + 4
n. -x + 3 > -2x + 12
o. 2(x - 9) > -3x +5
p. -(x - 9) < x -12
q. | x + 4 | ² 7
r. | x - 3 | > 5
s. -2x + 6 > -5
t. 2x - 6 > -5
u. | -x + 3 | = 4
v. -x + 6 > -(2x +5) and 4x > x +2
w. | x | = 9
x. | x - 4 | = 7
2. Sketch the graph of the following equations: (If the equation represents a line show, if possible, the x and y intercepts; for circles show the center (and compute the length of the radius) and 4 points on the circle.)
a. x = 5
b. y = -3
c. x + 2 y = 8
d. y = -x + 9
e. x2 + y2 = 16
f. x2 + y2 - 8x = 0
g. x2 + y2 + 4y - 6x = -2
h. (x - 4)2 + (y + 6)2 = (1/4)2
i. x/3 + y/7 = 1
j. -x + 3y = 9
k. 2x2 + 12 x + 2y2 - 8y = 3
3. Write down the following using interval notation:
a. -1 < x
b. x > 3
c. -2 < x < 9
d. x ³ 4
e. -2 < x ² 5
f. 3 ² x ² 9
4. Write down using inequalities the points which are represented by the following intervals (and draw a sketch of the interval:
a. (-2, 1)
b. (-6, -2 ]
c. [ 6, 8 ]
d. (-°, 5)
e. (6, ° )
5. Find the center and radius of the following circles and be prepared to draw a sketch of the circle which shows as least 4 points on the circle.
a. x2 + y2 = 100
b. x2 + y2 - 4x + 8y = -4
c. x2 - 6y + y2 + 10x = +2
d. x2 - y2 + 6y = -2y2
6. Given the function defined by the formula y = f(x) = -x2 + 4.
(i) Compute:
a. f(3)
b. f(-2)
c. f(0)
d. f(-1/2)
e. f(a)
f. f(a +1)
g. f(x +h) - f(x)
ii.
What are the domain and range of f(x).
7. Given the function defined by the formula y = g(x) = -
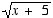
a. g(3)
b. g(-2)
c. g(0)
d. g(-1/2)
e. g(a)
f. g(a +1)
g. g(x +h) - g(x)
ii. What are the domain and range of g(x).
8. Given the function defined by the formula y = h(x) = x/(x-2)(x-4)
a. h(3)
b. h(-2)
c. h(0)
d. h(-1/2)
e. h(a)
f. h(a +1)
g. h(x +h) - h(x)
ii. What are the domain of h(x).
9. Sketch the location of the points (-2, -3), (-3, 2), (-4,2), (4, 5).
10. Given triangle O = (0, 0), A = (-3, -4) and B = (5, 12), find the lengths of the sides of the triangle and its perimeter. Write down the equations of the sides of this triangle.
11. Are the functions f(x) = 3x with domain the set of integers and the function g(x) = 3x with domain the real numbers the same?
12. Are the functions g(x) = | x - 4 |, domain all real numbers and h(x) = | 4 -x | domain all real numbers the same function?
13. For the function f(x) = 2x2 compute the value of f(x + 3) - f(3).
14. For the function f(x) = 9x compute the value of f (x +4) - f(4).
15. Be able to the use the vertical and horizontal line tests to determine the domain and range of a function which is defined with the use of a diagram showing the graph of the function.
15.
a. Write down the equation of the line given the points:
i. (0, 3) and (-4, 5)
ii. (0, 3) and (0, -11)
iii. (-2, -5) and (-1, -3)
iv. (-2, 0) and (2, 7)
b. Find the slope (if defined), intercepts, and two points on the lines below:
i. x + 3y = 7
ii. -3y = 7
iii. 2x + 5y = 11
iv. -5 x = 7
v. -3x + 6y = -5
16. Find the equation of a line parallel to 2x + 5y = 7 and which goes through the point (1,2).
17. Find the equation of a line perpendicular to 2x + 5y = 7 and goes through the point (1, 2).
18. Sketch a graph of the following equations:
a. y = 2x2
b. y = -2x2
c. y = 2x2 + 4
d. y = 2(x+3)2
e. y = -2(x-5)2 + 4