
Election: Reversing Ballots in Elections Decided by Positional Methods
Prepared by:
Joseph Malkevitch
Mathematics Department
York College (CUNY)
Jamaica, NY 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Consider the set of ballots below:

Using plurality we have:
A = 7, B = 4 and C = 3, which corresponds to a plurality ranking for society of:

Now let us reverse all of the voter ballots in the election above, which you can check gives:
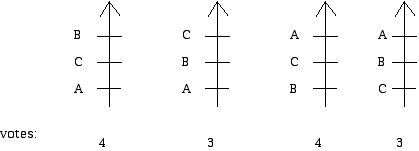
Now, again using plurality, A gets 7 votes, B gets 4 votes, and C gets 3 votes which means that societies ranking when the ballots are completely reversed is:

Perhaps, unintuitively, the society ranking stays the same between the original election and the election with reversed ballots!
You may wish to apply the anit-plurailty method to the original election. In anti-plurality one ranks on the basis of last place votes. A has the largest number of last place votes 7, so A will be ranked last. The person with the next largest of last place votes is B, and A has the fewest last place votes. So the anti-plurality ranking would be:

If one applies anti-plurality to the reversed ballots, we get the same ranking above, as the ranking for the election with reversed ballots. This is another unintuitve result.
Both plurality and anit-plurality can be interpreted as methods where points are given on the basis of first place, second place, etc. rankings by the individual voters.
It turns out that the only point count method that does not give a paradoxical result here is the Borda Count. For the original election the Borda Count values for A, B, and C are 14 points for each. Thus, there is a three way tie. For the reversed ballots, we again get A, B, and C with 14 points, so there is a three way tie again.
Reference:
Saari, D., and S. Barney, Consequences of Reversing Preferences, Institute for Mathematical Behavioral Sciences, University of California Irvine, Paper 30, 2003.