Measurement Activities for College Students
prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Science
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Note: Many of the problems below do not have a unique answer because the answer will depend on the assumptions made in doing the calculations.
Some problems related to daily life:
1. You are planning to drive by a direct route from New York City to San Francisco and back.
a. Estimate how far you will have to drive in miles.
b. i. Estimate how many gallons of gasoline this trip will require if your car is: a gas guzzler; a fuel efficient car.
ii. Compare the cost of your trip using a gas guzzler vs. a fuel efficient car using the current cost of gasoline in NYC.
c. If you took a trip of the same distance in Europe, you would measure the length of your trip in kilometers. Determine how many kilometers your trip would be.
d. If you take a trip in Europe, the gas you use would be measured in liters. How many liters of gas would you need for your trip if your car is: a gas guzzler; a fuel efficient car.
e. How many miles per gallon does a typical family car get in the United States?
f. How many kilometers per liter does a typical family car get in the United States?
g. How many kilometers per liter does a typical family car get in Europe?
h. How many miles per gallon does a typical family car get in Europe?
i. What is the typical current price of a gallon of gasoline in the United States?
j. What is the typical current price of a liter of gasoline in Europe?
k. How much would it cost for your round trip to San Francisco in euros at the current exchange rate between euros and dollars as computed in b. ii above?
l. How much would it cost for a similar round trip (same distance) in Europe using a car getting typical fuel efficiency in Europe, expressed in Euros and in dollars?
2. You are planning a nonstop airplane trip from New York City to Moscow. How far will the plane you take fly in taking such a round trip, assuming a shortest distance route is taken? What geometric issue needs to be taken into account for this question which does not have to be taken into account for the driving distance between New York and San Francisco?
3. Estimate the number of gallons of aviation fuel that must be used for a trip from New York to Moscow? What is the cost of fuel for an airplane to fly from New York to Moscow?
4. Twelve students rank their mathematics professor's teaching using the scale:
1=poor; 2=not as good as so-so, 3= so-so; 4=not as good as excellent; 5 = excellent
The scores a mathematics professor gets are: 1, 5, 2, 2, 2, 5, 4, 4, 2, 4, 4, 1.
The scores an English professor gets are: 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3.
The scores a psychology professor gets are: 2, 2, 5, 2, 5, 5, 2, 2, 2, 5, 5, 5.
Can any conclusions be reached about the relative merits of these three individuals as teachers?
5. A juice manufacturing company markets juice in cylindrical cans. The company currently markets a can which is 6 inches high and has a radius of 3.
If the company would like to make a "giant" size which contains twice as much juice:
a. What are some different sized cans that will achieve this goal?
b. Is there some "optimal" sized can(s) the company might consider?
Some problem solving (somewhat artificial) questions:
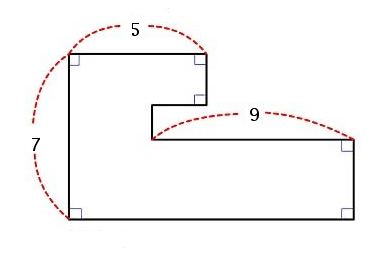
1. a. Find the perimeter of the region below assuming all the interior angles of the polygon shown are either 90 or 270 degrees.

b. What are the dimensions of a rectangle which has the same perimeter as the figure above and one of whose edges has length 7?
2. Is it possible to cut a piece of cheddar cheese which is a perfect cube (with side length one) with a plane so that the cross section is a regular hexagon? If so, what is the area and perimeter of this hexagon?
3. (Based on a problem of Martin Gardner)
Suppose that the earth were a true sphere. Suppose a thin railroad track tightly girdles the earth at the equator. If a yard of track is added to this "belt," how high above the earth will the track now "float?" (Measure this height in terms of what length has been added to the radius of the of the earth.)
Suppose we repeat this "experiment" for the sun. Suppose a thin railroad track tightly girdles the sun. (This is a nifty trick because the sun is gaseous and very hot.) If a yard of track is added to this "belt," how high above the sun will the track now "float?"
Some of the goals that should be accomplished via these activities are:
1. Conversion between different English and metric measurements, and even within the English system:
a. Miles to kilometers
b. Gallons to liters
c. Quarts to litters
d. Feet to yards
2. Different kinds of measurement scales:
a. Ratio scales
lengths, weights, and times
b. Interval scales
temperature, heights with respect to sea level
c. Ordinal scales
d. Nominal scales
3. Relative versus absolute differences
4. Measures of optimality
a. maximizing a minimum
b. minimizing a maximum
c. minimizing or maximizing a sum (or mean)