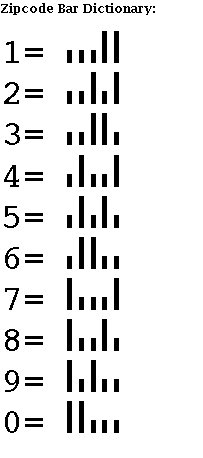Adventures in Geometry for First Graders (9/20/99)
Joseph Malkevitch
Department of Mathematics and Computing
York College (CUNY)
Jamaica, New York 11451
Email: malkevitch@york.cuny.edu (for additions, suggestions, and corrections)
Dear Parents,
At the brink of a new century, more mathematics has been created in the last 100 years
than in any other similar period in history. Not only has this tremendous growth
of mathematics transformed mathematics itself, with branches of mathematics in full
flower (e.g. dynamical systems, theory of knots, etc. ) that were barely investigated
100 years ago, but also applications and technologies made possible by mathematics
have become parts of our every day life. Fuel efficient cars and aircraft, fax machines,
CAT scans, audio compact discs, the World Wide Web, and high definition television
(HDTV) which commenced in November, 1998 are all gifts to society of work done
in mathematics during the 20th century. Unlike other areas of knowledge that require
reconsideration of what has become dogma due to a new experiment or a chance discovery,
once a mathematical theorem has been proven, it remains a fact. That the results
of mathematics are immutable creates a challenge for educators: how to blend the
amazing new results that are being discovered with the still important traditional body of
knowledge? The surprising thing is that many new mathematical results discovered
in the 20th century can be understood without many years of technical study. As a
result many of these new discoveries are being taught in mathematics and mathematics education
classrooms around the nation. However, most of these new ideas have not trickled
down into the elementary schools.
Historically, mathematics was taught as a series of progressions of techniques: arithmetic,
algebra, geometry, trigonometry, pre-Calculus, Calculus, etc.. In recent years,
however, a different approach is emerging. Mathematics can also be viewed not as
a hierarchy of technical topics but as a subject concerned with various themes
. These themes include: optimization problems (e.g. what is the cheapest way to collect
coins from pay phone booths), fairness problems (what are the fair ways for communities
building a new water treatment plant to share the savings due to cooperation), information (ways to hide, compress, track, correct, and synchronize information),
risk (is it riskier to use Viagra or to drive your car), unintuitive behavior (could
widening a road or opening a new road make congestion worse?), etc.
My goal here is to allow you and your children to share the excitement of seeing some
of these newer concerns of mathematics. As parents we know that in kindergarten and
1st grade students are learning to read and we are excited to share with them this
new adventure. However, all too often parents are unable or unwilling to share with their
youngsters the excitement of the child's first explorations with mathematics. This
is sad, since mathematics can open up for us all no less exciting intellectual vistas
than reading. It is in this spirit that the attached activities dealing with "information"
have been developed. The 19th century was marked by the industrial revolution. The
second half of the 20th century has been marked by the "information" revolution.
Mathematicians have been equal partners with engineers, physicists, and other scientists
in exploring and developing this revolution.
The activities below are designed for you to do in conjunction with your first grader
(though the ideas involved are of interest to the curious of all ages and educational
attainment). However, in addition to the activities themselves which I have provided for you to do with your child, I have also provided additional background information
that will give you a better perspective of how these activities relate to mathematics.
Enjoy!
References (for parents)
[1]. Kahn, D., The Codebreakers, Macmillan, New York, 1967.
This is the classic account of secret codes and how they have changed history.
[2]. Truxal, J., The Age of Electronic Messages, McGraw Hill, 1990.
This is a gentle introduction to the science, mathematics, and engineering principles
that are involved with many of the new developments in communications.
[3]. Wrixon, F., Codes and Ciphers, Prentice-Hall, New York, 1992.
This book is organized in dictionary form and contains a variety of information about
codes.
A book which contains information about codes, together with a wide variety of other
applications of mathematics is:
[4]. For All Practical Purposes, W.H. Freeman (only the 3rd, 4th, and new 5th editions have
information about codes).
Note:
The children's sections of many libraries usually have many books about secret codes.
Though mathematics is rarely explicitly involved in the discussions in such books,
there are many implicit ideas that are useful in building mathematical skills.
Remark:
Experts in cryptography (the science of designing and studying codes) make a distinction
between codes and ciphers. In a cipher, one symbol is consistently used to represent
a single letter (or number) in obtaining an enciphering of the information. For example, c used to represent a, d to represent b, e to represent c, ..., y to represent
a, and z to represent a is a typical example of what is called a substitution cipher.
In a code, typically a block of symbols consisting of 5 numbers or letters is used
to represent a word or group of words. One advantage of ciphers is that they are often
simpler to implement. Codes usually require the distribution of elaborate books which
show how different words and patterns of words are encoded or decoded. In the discussions here, the distinction between codes and ciphers is not rigorously maintained.
Activity 1
Reading the "bars" on your mail
Obtain an envelop which shows the bar pattern used for sorting mail. (Ideally, use
one which has the zipcode of your house (apartment building) on it.) You can do this
by finding an envelop from a bank addressed to your house. A sample is provided below.
Assuming the zipcode uses the ZIP + 4 system it would consist of 52 short and long
bars. This is known as the postnet code and is still commonly used on business reply
forms. (Sometimes only the bars for the original 5-digit zipcode is shown.) However,
starting in 1993, to take advantage of lower rates associated with the use of ZIP + 4,
businesses were required to use a 12-digit bar code known as the deliver-point bar
code. This takes the form of the ZIP + 4 code, followed by the two digits which are
the last two digits of the street address or postal box where the letter is headed. The
bar encoding for this system consists of 62 short and long bars. Thus, if the letter
addressed to your house shows the full 9-digit zipcode and was sent using a meter
system, the bar representation will nearly always have the 62-bar pattern.
Procedure:
Step 1: Erase the initial (first) long bar and terminal (last) long bar, to obtain
a sequence of 60 short and long bars. These extra bars, known as guard bars, are
present to assist the laser which scans the bar code locate the start and end of
the zipcode's bars.
Step 2: Group these 60 bars into groups of 5 bars starting from the left. (One obtains
12 groups of 5 bars.)
Step 3: Decipher each group of 5 bars into the digit it represents using the the table
(deciphering table) below (see page 6).
(What you should obtain is 11 digits. The first 5 of these are the usual zipcode which
codes the municipality that you live in (11530 for Garden City, New York) and the
next four numbers, in the suburbs, represents a code for a specific house (or apartment building or business). In New York City the additional 4 digits may represent a building
or even a floor of a building. Finally, the last two of the 11 digits should be the
last two digits of your street address (or that of the apartment building you live in or postal box that you use).
Puzzle:
Can you figure out how the 12th digit you obtain was chosen? (Remember that your zipcode
only uses 11 digits which can be coded using 55 bars.) For what purpose do you think
this last digit is present? (Note if you are using an envelop where there are only 50 bars after the guard bars are removed, can you figure out how the 10th digit you
obtain was chosen?)
Hint:
Step 4: Assuming you started with a 60-bar code (after the guard bars were removed),
have your child add up the 11 digits that have been decoded and add on the last digit.
Do you notice any pattern? (In order to guess the pattern you might have to try several different 60-bar code patterns. All mail that comes to your home will have the
same pattern so you need to try a code obtained from a relative or friend!) Note:
The same system is used in arriving at the 12th digit for a 60-bar code as is used
to get the 10th digit for a 50-bar code.
Note: The solution to the puzzle is given at towards the end!
Warning:
In mail addressed to private homes the bar code imprinted by the post office on the
envelop nearly always corresponds to the actual zipcode digits that are shown. However,
on some business reply envelops the bar code pattern sometimes does not actually
code the zipcode digits shown. This seems to be done by the companies involved to help
distinguish between mail which which is being paid for by the company and mail which
is being paid for by the sender.
Zipcode Bar Dictionary:
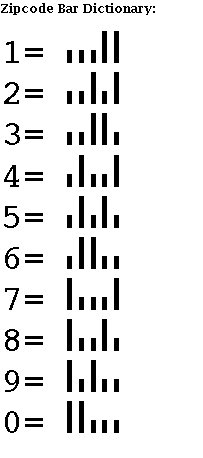
Figure 1
Example (no check digit included):
11530 =

Figure 2
Note:
The counting system that we ordinarily use is called decimal
because it uses ten symbols for digits (e.g. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) together
with place notation (e.g. 12 is different from 21). In the decimal the number one
hundred twenty is represented: 120. Using the decimal system we can represent arbitrarily large numbers. The same, however, can be said of the place notation system called
binary
, which uses only two symbols. When one counts in binary the way one counts from zero
to 9 is: 0, 1, 10, 11, 100, 101, 110, 111, 1000. In binary the number 120 is represented: 1111000
If one "pads" the representations of the digits from 0 to 9 on the left to result
in 5 digits one obtains: 00000, 00001, 00010, 00011, 00100, 00101, 00110, 00111,
01000. Note that these are not the 5-digit binary sequences used to represent 0-9
above. The reason for this is to note that what is given above is not the counting sequence representation
for the numbers from 0 to 9 but a code for the numbers from 0 to 9. This code has
binary sequences of five digits exactly two of which are ones. You can check that there are exactly 10 of these. The numbers are assigned, lexicographically, that
is, as if one were constructing a dictionary for them where 0 is considered to come
before 1.
Activity 2
How can we send secret messages?
To send a message use:
REPLACE:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
BY:
E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
EXAMPLE:
Plaintext (Message): MY NAME IS ALEX Coded text: QC REQI MW EPIB
To decode a message use:
REPLACE:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
BY:
W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
DECODE:
Coded text: GER CSY GSQI XS QC LSYWI WEXYVHEC?
Here are some additional messages to practice decoding using the same system as above.
i. QC XIEGLIV MW QVW WQMXL
ii. M PSSO JSAEVH XS KSMRK XS WXIAEVX WGLSSP
You may want to change the encryption system. Note that above, once the original code
is decided on, the decoding goes more easily if one writes down a separate decoding
table with the letters that are to be decoded listed in alphabetical order. Of course, one does not have to do this. Instead, with practice one can read the encryption
system "in reverse." Note that what makes systems such as this work is that corresponding
to each letter of the alphabet (making up the plaintext) there is one and only one
letter assigned to it in constructing the cipher.
One classical way to send secret messages is to systematically replace each letter
of the alphabet with another letter of the alphabet. A special case of these so-called
substitution
ciphers are the Caesar Ciphers (named to honor Julius Caesar who is reputed to have
used such a system). These are the special substitution ciphers obtained by "rotating"
the alphabet in deciding which letter should be used to represent another letter.
A complete set (rotating by 0 letters, which does not give a very safe system!, rotating
by 1 letter, ..., rotating by 25 letters) of the Caesar Ciphers is shown below in
the Vigenere Table (see appendix, pg. 16). The innovation of Vigenere was not to
use one of the Caesar Ciphers but to chose a KEY word and use it to determine a different
Caesar Cipher to encipher each letter of the original text (usually called the plaintext)
in turn. When one gets to the end of the key word, if there is still more plaintext, one starts over at the beginning of the key word. The Caesar Cipher to use from
the Vigenere Table is the row
which begins with the letters in the key word in turn. Once the row is chosen, the
way to encipher the particular letter involved is to find that letter's column at
the top of the table and read off the enciphered letter from the row chosen. If the
key word is known to the recipient, he/she can decode the message. This approach leads to
encipherments which are much harder for an intruder to break. In particular, the
same letter in the plaintext is typically enciphered using different letters.
Example: To encode the message LOCUST SCHOOL with the key word SMITH, the result would
be: DAKNZL EKBVGS
To make ciphered messages harder to read it is traditional to break up the text into
blocks of 5 letters (adding "nulls" -uncommon letters at the end if necessary to
fill out the end block to 5 letters). This system makes it harder to locate short
words such as "I," "IN,", "TO," etc.
It may appear that using a key word and the Vigenere table would lead to unbreakable
codes. This turns out not to be true. If one has large amounts of coded text that
have been coded with the same key one can use methods involving statistics to break
the code. With traditional ciphers the only way to send a totally secure message is through
the use of a randomly generated random key which is used only once. This system is
cumbersome. The recent development of public key cryptography (circa 1975) has led
to totally secure systems under the assumption that certain mathematical processes are
computationally as difficult as they appear to be. However, in many cases the computational
difficulty of the processes involved is not actually known. Recent improvements in algorithms (procedures) for factoring large numbers and the increased speed of computers is straining the safety of the early implementations of public key cryptography. For example, without too much effort a 155 digit number was factored into the two primes which gave rise to it.
Finally, the major use of codes up until the 20th century was security in the political
arena (e.g. spies use codes). However, with the development of modern communication
techniques, businesses have become the major users of encryption. When data is sent
over a phone line, or via radio waves to and from a satellite hookup, one wants to
be certain that the information is secure. In particular, banking and credit card
transactions should be secure. Modern mathematics has developed new methods that
are increasingly secure. Ironically, such developments have their negative aspects. For example,
coding systems now coming into use for cellular phones are so secure that law enforcement
officers worry about whether or not they will be able to control drug trafficking and other criminal activities if some system is not put in place which prevents
the best encryption systems from being used in cellular phones and other modern communication
equipment. Government regulations currently prohibit American companies from selling certain types of encryption equipment abroad, though it is probably foolish
to believe that Europe, say, does not have mathematicians as good as those in America
to design their own secure encryption systems!
Activity 3
How are pictures sent through a wire or space?
The picture below was sent to you by a friend from OUTER SPACE!
00000000000000000000000000000000000000001110011100000001110011100000001110000000000001110000000000001110011100000000000000000000000000011100000001110000000000000000011100000000000000000111000000011100000000000000000000000000011100000000000000000
STRANGE! It does not look like a picture. That is because the picture was sent in
code.
1. Can you figure out what what the picture is? It was encoded using the following
system:
BLACK CELL = 00000
RED CELL = 11100
BLUE CELL = 00111
YELLOW CELL = 11011
and fits into a 7x7 square grid (see appendix, page 17) starting with top left cell,
moves across the top row and when one gets to the end of a row, start at the beginning
of the next row. The more square grid cells that are used the more accurate is the
picture you get. However, this requires more symbols to send the picture which increases
transmission time.
Here are instructions for how to do this:
Step 1: Separate the binary digits into groups of 5.
Step 2: For each block of 5 digits determine which color this cell should be.
Step 3: Color the cells with the proper colors based on the received strings, starting
with the top left cell and moving across the rows, starting at the left of the next
row when you reach the end of a row.
By a miracle, there was no interference when this picture was sent. Every binary digit
that was sent arrived accurately! Unfortunately, with the second picture your space
friend had some transmission problems. HOWEVER, DO NOT WORRY. Your space friend
used an error correction code! (These are codes which make it possible to correct errors
that may have occurred during the transmission of the picture.)
Here is the picture that arrived using the same code as above:
00000000001110011100111000000000000000011110100000000000000001100100001010000001001111000000111100000000111100000011000011011000000000011100011000000000000100000000110000111001110000001110111101111011000011111000001111001110011100111001110000001
Here is the idea needed to draw the proper picture. It was discovered by Richard Hamming,
a great American mathematician who died recently.
We will find the DISTANCE between two binary strings of the same length, today called
the HAMMING DISTANCE, in honor of Richard Hamming. To find the Hamming distance,
merely count how many positions the two strings differ in!
Examples:
X means differ:
11100 00000 00010
00011 10100 00100
xxxxx x x xx
distance 5 distance 2 distance2
11111 00001 10101
11111 10001 10101
x
distance 0 distance 1 distance 0
Image decoding procedure:
Step 1: Separate the binary digits into groups of 5.
Step 2: If a block of 5 digits corresponds to a code word one knows immediately what
color that cell should be (using the color code above, page 11). However, if the
5 binary digits do not correspond to a code word we proceed as follows: Compare the
5 binary digits with each of the code words in turn, thereby computing the (Hamming) distance
between the received string and the code words. Assign the color for that 5-digit
string to the code word for which the Hamming Distance is as small as possible.
Example:
Suppose that 11000 is received from outer space. This string does not correspond to
any of the code words: 00000, 11100, 00111, 11011. Hence we find the Hamming Distance
between 11000 and each of the code words:
11000 11000 11000 11000
00000 11100 00111 11011
xx distance 2 x distance 1 xxxxx distance 5 xx distance
5
The smallest distance between 11000 and a code word occurs for 11100 which is red,
so we color the cell corresponding to the received string 11000 red!
Step 3: Color the cells with the proper colors based on the received strings, starting
with the top left cell and moving across the rows, starting at the left of the next
row when you reach the end of a row.
Note:
To send a picture from space or to send a picture via a cable system or satellite
hookup, the idea is to break up the image into a rectangular grid of small cells
called pixels. (Pixel is short for picture element.) The potential light intensities
(or the intensities and color separations for three colors) that might occur are each assigned
a binary symbol as a code. The codes for each pixel of the image are sent to represent
the original picture. Modern codes for representing the pixels in an image are chosen to achieve additional goals other than the mere transmission of the image. These
codes as seen above can correct errors and they also can be used to compress images.
A collection of 8 binary digits is typically called a byte.
If a byte is used to represent an intensity, one can code 256 different levels of
intensities using a byte. However, as we saw above the key to error correction is
having code words whose pairwise Hamming Distance is large. If every pair of code
words has distance at least 3 one can correct one error per code word, while if the pairs of
code words are at least distance 5 apart one can correct 2 errors. The problem facing
mathematicians is to design as large a collection of code words as possible which
have few binary digits and are as far apart as possible! Not surprisingly this is a difficult
task. It is known, for example, that using binary sequences of length 12 one can
use 256 code words and correct one error; however, for length 12 code words which
correct two errors, the largest number of code words is 32. The issue of how much error
correction capability one needs in the code depends on how "noisy" the environment
is in which the code is being used. A code which might work well for a compact audio
disc might not be suitable for sending pictures back from deep space.
Solution to Puzzle in Activity 1.
The sum of all ten digits always ends in a ZERO. In fact, the last digit is always
chosen so that the final sum ends in a ZERO.
The tenth digit provides an example of a "check" digit. It was built into the design
of the system so that errors can be either detected or corrected. Errors occur from
time to time due to, in the case of a zipcode, a human or a laser reader error. If
the last digit in the final result does not make the sum of the digits end in a zero (i.e.
be divisible by 10), then one knows that an error has occurred. Thus, the system
for zipcodes is an error detection system. Similar check digit systems are incorporated in the ISBN system of providing numbers for books, the UPC (Universal Product Code)
which is the bar code system used on the items you purchase at a store, the routing
codes used on your checks, and the tracking codes used by Federal Express and UPS
to make sure that your letters or packages can be delivered reliably.
The use of error detection and, even better, error correction systems are now a standard
part of digital technology. Codes are used in sending fax transmissions, pictures
from the Hubble telescope, in audio compact discs that detect and correct errors
that occur during the processing of the images or sounds. It has also become standard
to employ codes to correct errors in computers, modems and telephone circuits. It
is important to understand the type of error being referred to here. If a computer
is expecting a block of symbols to be one of the binary sequences from a certain list (the
symbols may represent gray levels of a picture) and the sequence that the computer
gets is not on that list, it can figure out the most reasonable item in the list
to use instead of the incorrect sequence.
Return to Joseph Malkevitch's Home Page