Combinatorial and Discrete Geometry: Sheet Q
Matchings in Bipartite Graphs
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York 11451
email: joeyc@cunyvm.cuny.edu
web page: http://www.york.cuny.edu/~malk
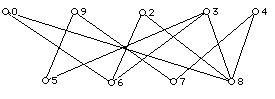
1. For each of the bipartite graphs below find the two sets systems (think of the top set of vertices as workers, and the bottom set of vertices as jobs for which the workers might be qualified) associated with the graphs:
G:

H:

I:

J:
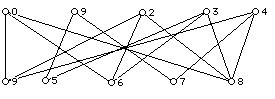
2. For each of the set systems, constructed from the graphs above, do they obey the Philip Hall "diversity condition?"
3. Find the largest number of workers who can be assigned to jobs for which they are qualified in the graphs above. If not all the workers can be assigned to jobs, can you find two different collections of workers, but the same number of workers, who can be assigned jobs?
4. Can any set of 3 workers for graph H be assigned to three jobs? (How many different sets of three workers are there in this example?)