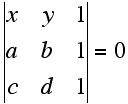
Geometric Structures: Practice 5: Desargues Theorem
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Given two points in the Euclidean plane, (a, b) and (c, d) we can write down an easy expression for the line which passes through these points using determinants:
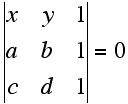
Remember that if two rows or columns of a determinant are equal then the value of the determinant is identically 0. Hence, above, if one substitutes for the x and y values x = a and y = b (or x = c and y = d) we get 0. Thus, the above determinant when expanded gives the equation of a line which passes through the points (a, b) and (c, d).
It should not surprise you, therefore, that using homogeneous equations in the real projective plane that:
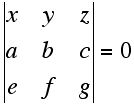
is the equation of a line that passes through the points (a, b, c) and (e, f, g).
Desargues' "statement" is:
Given two triangles a projective plane, ABC and A'B'C',
if:
the lines AA', BB' and CC' pass through a single point
then
given
X = the point where AB and A'B' meet
Y = the point where AC and A'C' meet
Z = the point where BC and B'C' meet
we can conclude that X, Y, and Z lie on a line!
Sometimes this theorem is described by saying:
if two triangles are in perspective from a point, they are in perspective from a line.
The converse of this theorem is also true.
If two triangles are in perspective from a line, they are in perspective from a point.
Desargues' statement is true in some projective planes and not true in others.
In the real projective plane it is true. It is also true for a projective plane embedded in a 3-dimensional space. Desargues statement is true in some finite projective planes and false in others. An example of an infinite projective plane in which it fails to hold is the Moulton Plane.
Here is an example/exercise to help you understand the issues involved for the real projective plane.:
Suppose that A = (3, 4, 1), B = (6, 0, 1) and C = (-1, 5, 1)
and A' = (1, 3, -(1/2)) B' = (0, -12, 1) and C' = (1, 9, 1).
1. Rewrite the coordinate of A' so that its z value is -1. Also, rewrite A" so that its z value is +1. Do any of these 6 points lie on the line at infinity for the real projective plane?
2. Find the equation of the line through A and A'.
3. Find the equation of the line through B and B'.
4. Find the equation of the line through C and C'.
5. Verify that the three lines (problems 2., 3., and 4.) all pass through a single point.
(If you have done the calculation properly you should find a point with Z coordinate 0. What slope do the corresponding lines to these three lines in the real projective plane have in the Euclidean plane? Is this what you expected?)
6. When lines meet at a point with Z coordinate 0 then these projective plane lines, when interpreted in terms of the Euclidean lines from which they are derrived, would all be parallel. Is this true for the lines that you found in 2., 3., and 4.?
7. Find the point where AB meets A'B'
8. Find the point where AC meets A'C'
9. Find the point where BC meets B'C'
10. Do the points you found in 7., 8., and 9., all lie on a straight line?
Hint: Some of this work will go faster if you use the determinant result above.
11. Consider the point 0 = (3, 4, 1) and the triangle A= (-1, 1, 1) B = (1, 3, 1) and C = (2, -4, 1). Pick any point third point on the line through OA as A'; pick any third point on the line through OB as B'; pick any third point on the line through OC as C'.
Now verify that Desargues' statement holds for the triangles ABC and A'B'C'. Note that if you carried out the process above properly, then the lines AA', BB', and CC' should all go through O!
Back to Geometric Structures page