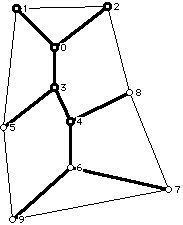
Figure 1
Geometric Structures: Session VII
More Loose Ends; Obtaining Graphs From Other Graphs; Plane Graphs
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk
The more experiments you do with drawing graphs the more you see the geometrical possibilities for exploring geometrical patterns in doing graph theory explorations, including finding microworlds to do proofs and finding connections with other parts of mathematics. Although a case can be made that all of graph theory, except for its most obviously algebraic aspects (there is a whole subpart of graph theory that deals with "algebraic" graphs), has significant geometric content, for plane graphs the geometry in the graph theory is very clear. Of course, the geometry has a somewhat combinatorial (non-metrical) and topological flavor but if nothing else, Euler's Polyhedra Formula and Steinitz's Theorems are writ large as topics in both graph theory and in geometry.
Given a graph G, one can find subgraphs of G by deleting a vertex v from the graph (G -v) or by deleting an edge e of the graph (G - e). When one deletes an edge one removes the edge but leaves its endpoints (endpoint in the case of a self-loop) intact. When deleting a vertex, one removes the vertex and edges which are present at the vertex. If removing a vertex increases the number of components of a graph (a connected graph has one component), then the vertex is called a cut vertex. If removing an edge of a graph increases the number of components of the graph, then the edge is called a cut edge or a bridge. (Remember that not all authors use the same terminology but the definitions above are pretty standard.)
For any graph H (for simplicity, say, without loops and multiple edges) there is an interesting way of creating a new graph known as the line graph L(H) of H. The idea is that for each edge of H one creates a vertex in L(H). One joins two vertices in L(H) if the edges they represent have a vertex in common.
Figure 1 shows a graph (which is planar but has not been shown in a plane embedding).

Figure 2 shows the line graph of the graph in Figure 1.
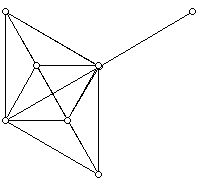
Do now 1:
a. Verify for yourself that the graph in Figure 2 is really the line graph of the graph in Figure 1.
b. Show that the graph in Figure 2 is planar by embedding this graph without accidental crossings in the plane.
In general, a plane graph's line graph will not be a planar graph - it might even be non-planar, meaning that no matter how hard one tries, one cannot redraw it in the plane without accidental crossings.
There several interesting ways to transform a plane graph into another plane graph. One of these is the geometric dual, which has been mentioned briefly in past notes. The idea is take a plane graph (again for simplicity, no loops or multiple edges or bridges) and place a vertex in the interior of each face. Now join two vertices by an edge if the faces they lie in share a common edge. When a dual graph is constructed, it can be done in a way such that each edge of the dual crosses exactly one edge of the original graph. Thus, a plane graph and its dual have an equal number of edges. However, if G has V vertices and F faces, then G* its dual has F vertices and V faces.
Figure 3 shows the graph of a triangular prism.

For plane graphs, there is a way to transform a plane graph into another plane graph which is in the spirit of the line graph. The transformed graph is known as the medial graph of the original. Place a dot (vertex) on each edge of the original graph. Now join two of these new vertices if the edges they represent in the original graph have a vertex of the original graph in common as well as being in the same face. Figure 4 shows the medial graph of the graph in Figure 3.

Note that the medial graph of any plane graph always results in a 4-valent graph. In particular, if the original plane graph is 3-valent, we can transform the graph into a plane 4-valent graph. Taking the dual of a 4-valent graph results in a graph for which all of the faces are 4-gons. If one wants a plane graph all of whose faces are 3-gons, this can be done by taking the dual of a 3-valent graph. In many cases the line graph of a plane graph will be neither 4-valent nor planar.
Other operations that can be done on a plane graph which to transform it into an interesting plane graph are:
a. Replacing every edge of a graph with a hexagon.
b. Transforming a graph all of whose faces are 4-gons into a graph all of who faces are 5-gons.
The two key results in geometry related to plane graphs are:
a. Euler's Polyhedral Formula, which in a general form says that for any plane graph which is connected V + F - E = 2.
b. (Steinitz's Theorem as reformulated by Branko Grünbaum and Theodore Motzkin) A graph G is isomorphic to the vertex-edge graph of a 3-dimensional convex polyhedron if and only if G is planar and 3-connected.
Do now 2:
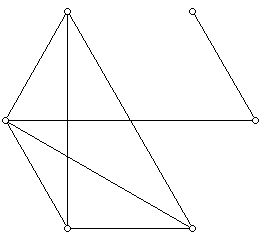
a. Is the graph below (Figure 5) isomorphic to the vertex-edge graph of a convex 3-dimensional polyhedron?
b. Is the graph below isomorphic to the vertex-edge graph of a non-convex 3-dimensional polyhedron?

Another nice way to construct graphs which are 3--polytopal is to start with a tree drawn in the plane which has at least 4 vertices and no vertices of valence two. Now pass a simple circuit through the 1-valent vertices of the tree. The resulting graph is 3-polytopal and is usually referred to as a Halin Graph, after Rolf Halin who studied graphs which arise in this way. In Figure 6 the dark edges are the original edges of the tree and light edges form the circuit through the 1-valent vertices. Halin graphs either are pancyclic or lack a circuit of one length. Pancyclic means having circuits of all lengths. Halin graphs always have Hamiltonian circuits.