Problem Set II (Geometric Structures - Spring 2011)

Prepared by:

Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451

email:

malkevitch@york.cuny.edu

web page:

http://york.cuny.edu/~malk

1. If G is a graph, a valence vector for G, (v₁, v₂, v₃, v₄, ... , v_max) is a non-negative integer vector where v_i is the number of vertices of G with valence i. If G is a plane graph embedded in the plane, a face vector for G, (p₃, p₄, ... , p_max) is a non-negative integer vector where p_i is the number of faces of G with i sides.

a. Can you find a graph with valence vector (4, 8, 6, 1)?

b. Can you find a graph with face vector (4, 8, 6, 1)?

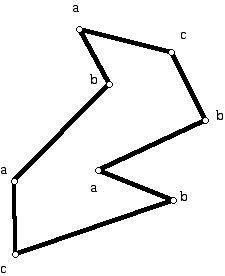
2. Given the simple polygon below:

a. Find the minimum number of vertex guards necessary to see all of this polygon.

b. Draw at least 4 inequivalent triangulations for this polygon and, using each of these triangulations, find the number of vertex guards that a 3-coloring of the triangulation determines.

c. How many guards placed in the exterior of this polygon are necessary to guard the exterior of the polygon?

3. Definition: A polygon is equilateral if all of its sides have the same lengths.

a. If possible draw a simple plane equilateral polygon with 6 sides which requires 2 guards.

b. If possible draw a simple plane equilateral polygon with 9 sides which requires 3 guards.

4. a. Sketch a diagram of the points whose Euclidean distance from (2, 2) and (6, 6) is the same.

b. Sketch a diagram of the points whose taxicab distance from (2, 2) and (6, 6) is the same.

c. Sketch a diagram of the points whose Euclidean distance from (0, 0) and (6, 8) is the same.

d. Sketch a diagram of the points whose taxicab distance from (0, 0) and (6, 8) is the same.

e. Sketch a diagram of the points whose Euclidean distance from (0, 0) and (2, 10) is the same.

f. Sketch a diagram of the points whose taxicab distance from (0, 0) and (2, 10) is the same.